Algoritmy a datové struktury 2

Při sepisování poznámek jsem hodně čerpala z Průvodce labyrintem algoritmů. Z knihy jsem přejala většinu značení a mnoho obrázků.

Prohledávání řetězců

• hledání podřetězců v řetězcích – „hledání jehly v kupce sena”

Značení

• $\iota$ – jehla

• $\delta$ – seno

• Σ – abeceda

• $\alpha , \gamma , \beta$ – slova/řetězce

• $a, b, c$ – znaky

• $|\alpha|$ – délka řetězce

• $\epsilon$ – prázdný řetězec

• $\alpha \beta$ – zřetězení řetězců $\alpha$ a $\beta$

• $\alpha [i]$ – i-tý znak řetězce $\alpha$

• $\alpha [i:j]$ – podřetězec řetězce $\alpha$ $[i, j)$

  • vynechání dolní meze – prefix
  • vynechání horní meze – sufix

Inkrementální algoritmus

• začínáme od prázdného řetězce a na konec přidáváme postupně znaky sena
  • Jaký je nejdelší prefix jehly, který je sufixem sena?

Knuth-Morris-Pratt algoritmus

• vyhledávací automat
  • vrcholy – prefixy jehly
  • dopředné hrany – přidání písmenka
  • zpětné hrany – kam se přesunout, když vyhledávání failne

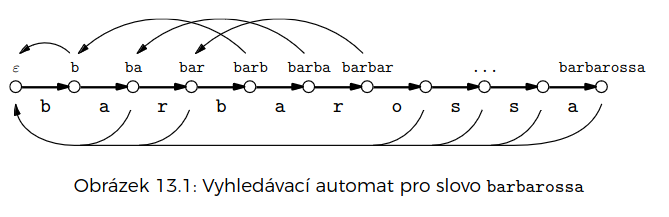
• v paměti můžeme reprezentovat buďto jako graf, nebo jako pole na zpětné hrany (na dopředné stačí samotná jehla)

• procházíme seno a chodíme jehlou po hranách podle znaků, na které narážíme

• pokud se dostaneme do koncového stavu, ohlásíme výskyt jehly a vrátíme se na začátek

• Stav sena je roven maximální délce prefixu jehly, která je sufixem zatím zpracovaného sena

Analýza složitosti

Lemma: Funkce $\text{KmpHledej}$ běží v čase $\Theta (S)$

• projdeme po nejvýše $S$ dopředných hranách (to ale neplatí pro zpětné hrany)
• každá dopředná hrana vede o právě 1 stav doprava a každá zpětná alespoň o 1 stav doleva
  • průchodů po zpětných hranách je nejvýše tolik, kolik dopředných – nejvýše $S$

Konstrukce automatu

• budeme stavět automat pomocí sama sebe (wha-…?)
• pořídíme si automat jen s dopřednými hranami a doplníme zpětnou hranu ze stavu 1 do stavu 0
• následně budeme doplňovat zpětné hrany pro další stavy
  • pro stav $\alpha $ můžeme v pohodě používat tento automat pro jehly délky $|\alpha |-1$
  • předhodíme tedy automatu ten samý stav bez prvního písmenka a tam kde skončíme, tam bude vést zpětná hrana ze stavu $\alpha$
    • nejlíp jde tohle pochopit, když si to člověk sám vyzkouší

Analýza složitosti

• spouštění automatu postupně na řetězce $\iota[1:1], \iota[1:2], \iota[1:3], \dots$ by nás stálo $\mathcal{O}(J^2)$
  • každý z těchto řetězců je prefixem toho následujícího – stačí spustit na $\iota[1:]$ a zaznamenávat postup

Aho-Corasicková

• $\delta$ – seno

  • $S = |\delta|$

• $\iota_1, \iota_2, ..., \iota_n$ – jehly

  • $J = \sum_{\begin{subarray}{l} \\i \end{subarray}} |\iota_i|$

• $V$ – počet výskytů jehel v seně

Automat

• stavy = prefixy jehel

• dopředné hrany: $\alpha \rightarrow \alpha x$

• konce jehel

• sestavíme si trii

• na ní postavíme stejné zpětné hrany jako na KMP

  • problém: co když bychom v senu došli do bodu, kde končí výskyty dvou různých jehel?
  • řešení: vytvoříme si zkratové hrany do terminálních vrcholů
    • Zkratková hrana ze stavu $\alpha$ vede do nejbližšího koncového stavu $\zeta(\alpha)$ dosažitelného z $\alpha$ po zpětných hranách (a různého od $\alpha$)

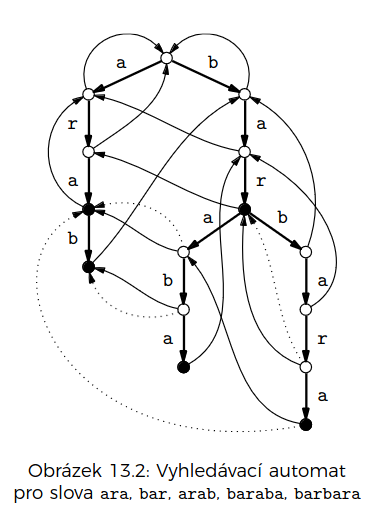
Reprezentace

• pro každý očíslovaný stav (0 = kořen, pak libovolně) automatu si pamatujeme:
  • číslo stavu, kam vede zpětná hrana
  • číslo stavu, kam vede zkratková hrana
  • zda tu končí nějaké slovo a pokud ano, které
  • kam vede dopředná hrana označená písmenem $x$

Algoritmus

Analýza složitosti

• počet dopředných hran, které projdu je nejvýše $S$
• počet zpětných hran, které projdu je nejvýše počet projitých hran dopředných (stejný argument jako u KMP)
• $\mathcal{O}(S)$

Konstrukce automatu

• zpětné hrany vedou napříč mezi různými jehlami
• musíme budovat po hladinách (BFS)
  • opět začneme jen s triviálními zpětnými hranami do nulového stavu
  • v každé iteraci algoritmu rozšíříme každou jehlu o jednu vrstvu následujících znaků

• konstrukce zpětných hran hledá všechny jehly, jen kroky jednotlivých hledání vhodně střídá
  • časová složitost je tedy shora omezena součtem složitostí hledání jehel – $\mathcal{O}(J)$
• počet projití po zkratkových hranách je roven počtu výskytů – $\mathcal{O}(V)$

Rabin–Karp

• pro hledání jedné jehly délky $J$ v seně délky $S$
• budeme posouvat okénko délky $J$ po seně a pro každý podřetězec si počítat hash
  • pokud se hash podřetězce rovná hashi jehly, zkontroluji lineárně, jestli je nalezený řetězec opravdu stejný jako jehla
  • problém: hashování je lineární

Hashovací funkce

• chceme hashovací funkci, která je schopna se přepočítat při posunutí okénka o jedno doprava v konstantním čase

• písmena jsou přirozená čísla $x_1,..., x_J$

• $P$ je nějaká vhodná konstanta

  • musí být nesoudělná s $N$ !!!
  • $P^J$ musí být řádově větší než $N$

• $N$ budeme chtít volit $> JS$ (odůvodnění později)

• při posunutí okénka o jedno doprava:

Analýza složitosti

• pokud si mocniny $P^J$ předpočítáme, proběhne aktualizace v $\mathcal{O}(1)$

  • inicializace v $\mathcal{O}(J)$

• v každé poloze okénka můžeme strávit až $\mathcal{O}(J)$ času

  • složitost $\mathcal{O}(JS)$ – au au

• řetězce porovnáváme když:

  • nastane výskyt
  • hash jehly se shoduje s hashem okénka (ač se řetězce nerovnají)
    • pravděpodobnost $\frac{1}{N}$ (za předpokladu dokonale náhodného chování hashovací funkce)

• v průměru tedy spotřebujeme čas $\mathcal{O}(J + S + VJ + J \cdot \frac{S}{N})$

  • inicializace + průchod senem + kontrola pravých výskytů + kontrola falešných výskytů

• pokud nám bude stačit najít jen první výskyt a $N > JS$, časová složitost bude v průměru $\mathcal{O}(J+S)$

Toky v sítích

• intuitivní představa:
  • síť trubek popsaná orientovaným grafem
    • hrany ohodnocené „kapacitami” – kolik tekutiny jimi může protéct za jednotku času
  • dva význačné vrcholy – zdroj a stok

Síť

Definice: Síť je uspořádaná pětice $(V, E, z, s, c)$, kde:

• $(V, E)$ je orientovaný graf

• $c: E \rightarrow \R^{+}_0$ je funkce přiřazující hranám jejich kapacity

• $z, s \in V$ jsou dva různé vrcholy grafu, kterým říkáme zdroj a stok

• o grafu budeme předpokládat, že je búno symetrický

  • $uv \in E \implies vu \in E$
  • pro hrany $uv$ bez $vu$ si jednoduše přidáme hranu $vu$ s nulovou kapacitou

Tok

Definice: Tok v síti je funkce $f: E \rightarrow \R^{+}_0$, pro níž platí:

1. Tok po každé hraně je omezen její kapacitou $\forall e \in E : f(e) \leq c(e)$.

2. Kirchhoffův zákon: Do každého vrcholu přiteče stejně, jako z něj odteče („síť těsní”).

   Výjimku může tvořit pouze zdroj a spotřebič. Formálně:

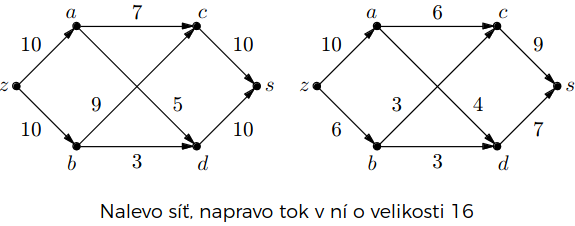
• celkový přítok do vrcholu: $f^+(v) := \sum_{u:uv \in E} f(uv)$

• celkový odtok z vrcholu: $f^-(v) := \sum_{u:vu \in E} f(vu)$

• přebytek ve vrcholu: $f^{\Delta}(v) := f^+(v) - f^-(v)$

• Kirchhoffův zákon: $\forall v \neq z,s : f^{\Delta}(v) = 0$

Lemma: $f^{\Delta}(z) = -f^{\Delta}(s)$

• mějme součet přebytků všech vrcholů $S = \sum_v f^{\Delta}(v)$

  • dle Kirchhoffova zákona může být přebytek nenulový pouze ve zdroji a spotřebiči

    • $S = f^{\Delta}(z) + f^{\Delta}(s)$

  • zároveň je to součet kladných a záporných toků po hranách, přičemž každá přispěje jednou kladně (ve vrcholu, do kterého vede) a jednou záporně (ve vrcholu, odkud vede)

    • $S = 0$

• $f^{\Delta}(z) + f^{\Delta}(s) = 0 \implies f^{\Delta}(z) = -f^{\Delta}(s)$

Ford-Fulkerson

• začneme s nulovým tokem a postupně ho budeme vylepšovat

• rezerva hrany $uv$: $r(uv) := c(uv) - f(uv) + f(vu)$

  • kolik můžeme ještě poslat tekutiny po směru a protisměru

• nasycená hrana: hrana s nulovou rezervou

• nenasycená hrana: hrana s kladnou rezervou

• nasycená cesta: cesta s alespoň jednou nasycenou hranou

  • touhle cestou už nemůžeme poslat více tekutiny (porušili bychom tak Kirchhoffův zákon)

• nenasycená cesta: cesta se všemi hrany nenasycenými

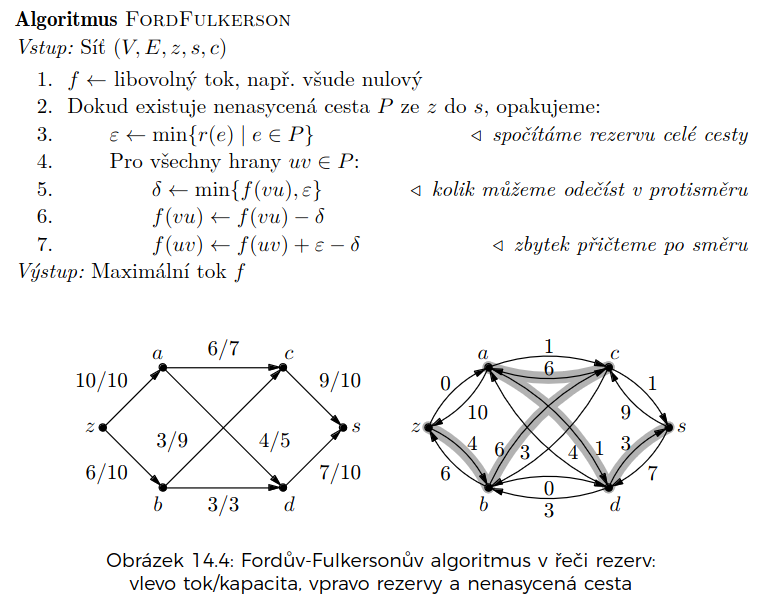
Konečnost

• algoritmus zachovává celočíselnost

• velikost toku se v každém kroku zvýší alespoň o 1

  • algoritmus se zastaví po nejvýše tolika krocích, kolik je horní mez pro velikost maximálního toku

• pro racionální kapacity stačí vynásobit velikosti všech hran nejmenším společným násobkem jejich jmenovatelů

• pro iracionální kapacity se nemusí algoritmus nikdy zastavit, ba ani konvergovat ke správnému výsledku

Analýza složitosti

• pro síť, jejíž jednotky jsou racionální a jejíž maximální tok je $f$, nalezne Ford-Fulkersonův algoritmus maximální tok v čase $\mathcal{O}(|f| \cdot m)$ ($m$ je počet hran)

  • nenasycenou cestu najdeme a zlepšíme v čase $\mathcal{O}(m)$ prohledáním grafu
  • každé prohledání zlepší tok alespoň o 1, počet iterací je omezen velikostí maximálního toku $|f|$

• pokud budeme v FF používat BFS, bude časová složitost $\mathcal{O}(nm^2)$​

  • této úpravě se říká algoritmus Edmonds-Karp, na jehož myšlence pak vznikl Dinicův algoritmus
  • hezké počtení o něm je zde

Maximalita toku

• pro důkaz využijeme řezy

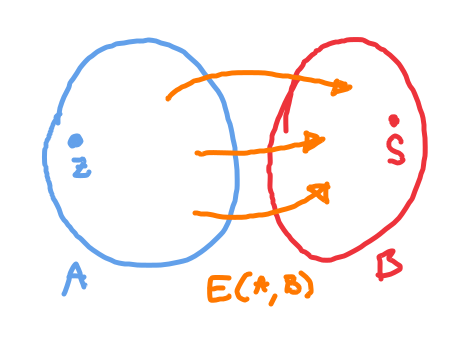
• $A$ a $B$: množiny vrcholů, které dohromady obsahují všechny vrcholy sítě a jsou zároveň disjunktní

  • v $A$ musí ležet zdroj $z$ a v $B$ stok $s$

• $E(A, B)$: množina hran vedoucích z $A$ do $B$ (elementární řez)

• $f(A,B) := \sum_{e\in E(A,B)} f(e)$ – tok z $A$ do $B$

  • počítám pouze hrany orientované z $A$ do $B$

• $f^{\Delta}(A,B) := f(A,B) - f(B, A)$ – čistý tok z $A$ do $B$

  • počítám i zpetný tok z $B$ do $A$

• Pro každý řez $E(A,B)$ a každý tok $f$ platí $f^{\Delta}(A,B) = |f|$

  • opět se odkazuji na Kirchhoffův zákon – co vyteče ze $z$, musí někam dotéct
  • pro důkaz stačí sečíst přebytky ve vrcholech

• díky tomuto pozorování můžeme měřit celkovou velikost toku na jakémkoliv řezu

Lemma: pokud se Ford-Fulkersonův algoritmus zastaví, vydá maximální tok

• nechť se algoritmus zastaví
• mějme množiny vrcholů
  • $A := \{v \in V | \text{existuje nenasycená cesta ze }z \text{ do }v\}$
  • $B := V \setminus A$
• množina $E(A, B)$ je řez
  • zdroj je v $A$ – ze $z$ do $z$ existuje nenasycená cesta délky 0
  • stok je v $B$ – kdyby nebyl, existovala by nenasycená cesta ze $z$ do $s$ a algoritmus by tedy ještě neskončil (spor)
• všechny hrany řezu $E(A,B)$ mají nulovou rezervu
  • po všech hranách řezu vedoucích z $A$ do $B$ teče tok rovný kapacitě hran a po hranách z $B$ do $A$ neteče nic
    • $E(A,B)$ je minimální $\implies f$ je maximální

Maximální párování

• párování – množina hran taková, že žádné dvě hrany nemají společný vrchol

• mějme bipartitní graf $(V, E)$ a přetvořme ho na síť $(V', E', z, s, c)$ takto:

  • rozdělíme graf na levou a pravou partitu
  • všechny hrany zorientujeme zleva doprava
  • přidáme zdroj $z$ a vedeme z něj hrany do všech vrcholů levé partity
  • přidáme stok $s$ a vedeme do něj hrany ze všech vrcholů pravé partity
  • všem hranám nastavíme jednotkovou kapacitu

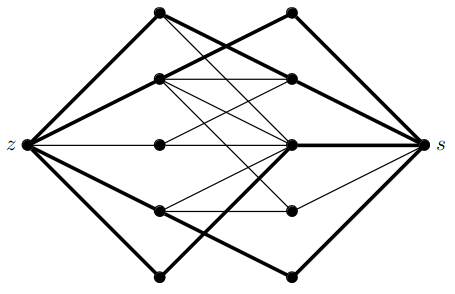
• v této síti pak najdeme největší celočíselný tok pomocí Ford-Fulkersonova algoritmu

• nalezené párování je největší možné

  • z toku vytvoříme párování o tolika hranách, kolik je velikost toku a naopak z každého párování umíme vytvořit celočíselný tok odpovídající velikosti
    • bijekce mezi množinou všech celočíselných toků a množinou všech párování, která zachovává velikost

Analýza složitosti

• pro síť, jejíž kapacity jsou jednotkové, nalezne Ford-Fulkersonův algoritmus maximální tok v čase $\mathcal{O}(nm)$ ($n$ je počet vrcholů, $m$ počet hran)
  • nenasycenou cestu najdeme a zlepšíme v čase $\mathcal{O}(m)$ prohledáním grafu
  • každé prohledání zlepší tok alespoň o 1, počet iterací je omezen velikostí maximálního toku, což je pro síť hran s jednotkovými kapacitami hran nejvýše $n$

Dinicův algoritmus

• zlepšuje tok pomocí jiného toku

Síť rezerv

• kapacita každé hrany je nahrazena rezervou při toku $f$

Definice: každé hraně přiřadíme její průtok $f^*(uv) = f(uv)-f(vu)$ (tok tam mínus tok zpět)

1. $f^*(uv) = - f^*(vu)$
2. $f^*(uv) \leq c(uv)$
3. $f^*(uv) \geq -c(vu)$ – plyne z předchozích dvou
4. pro všechny vrcholy $v \neq z, s$ platí, že $\sum_{u:uv \in E}f^*(uv) = 0$
   • opět Kirchhoffův zákon – co přiteče hranami dovnitř, vyteče hranami na druhé straně ven
   • stejný vztah jako pro přebytek $f^{\Delta}(v)$ popsaný ve FF alg.
   • $f^*(uv) = -f^*(vu)$

Lemma P (o průtoku)

• pokud funkce $f^* : E \rightarrow \R$ splňuje podmínky $(1)$, $(2)$, $(3)$ a $(4)$, pak existuje tok $f$, jehož průtokem je $f^*$.

  • tok $f$ určíme pro každou dvojici hran $uv$ a $vu$ zvlášť

  • předpokládejme, že $f^*(uv)\ge0$

    • pak $f(uv):=f^*(uv)$ a $f(vu):=0$
    • díky $(2)$ funkce $f$ nepřekračuje kapacity a díky $(4)$ pro ni platí Kirchhoffův zákon
      • je to tok

Lemma Z (o zlepšování toků)

• pro každý tok $f$ v síti $S$ a libovolný tok $g$ v síti rezerv $R(S, f)$ lze v čase $\mathcal{O}(m)$ nalézt tok $h$ v síti $S$ takový, že $|h| = |f| + |g|$.

  • nemůžeme sčítat přímo toky, ale můžeme sčítat průtoky po jednotlivých hranách
    • $h^*(uv) := f^*(uv) + g^*(uv)$

  1. podmínka $(1)$ platí pro $f^*$ i $g^*$, tudíž platí i pro jejich součet

  2. víme, že $g^*(uv) \leq r(uv) = c(uv) - f^*(uv)$, tudíž $h^*(uv) = f^*(uv) + g^*(uv) \leq c(uv)$

  3. stejný důkaz jako pro $(2)$

  4. když se sečtou průtoky, sečtou se i přebytky

Definice: Tok je blokující, jestliže na každé orientované cestě ze zdroje do spotřebiče existuje alespoň jedna hrana, na níž je tok roven kapacitě

• v řeči FF – všechny cesty jsou nasycené

Definice: Síť $S$ je vrstevnatá (pročištěná), pokud každý vrchol i hrana leží na nějaké nejkratší cestě ze $z$ do $s$

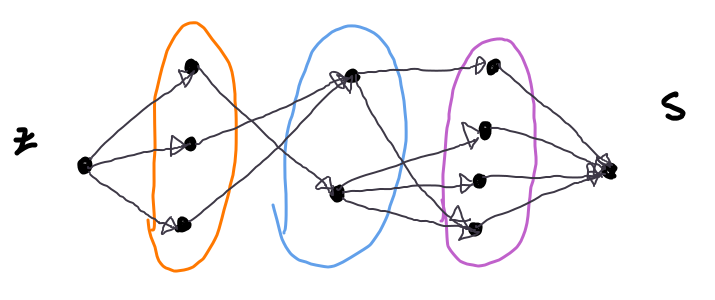
• $f$ je maximální tok, protože na konci neexistuje cesta s kladnou rezervou, což odpovídá momentu, kdy se zastaví FF algoritmus, který pokud se zastaví, určitě vydá maximální tok (což už jsme si dokázali)

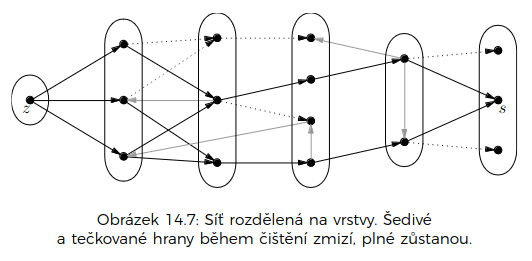
• čištění sítě je celkově v $\mathcal{O}(m)$
  • každou hranu odstraním nejvýše jednou… duh
  • smazaných vrcholů je nejvýše tolik, kolik je smazaných hran

• algoritmus pro hledání blokujícího toku odpovídá prvnímu naivnímu hladovému algoritmu pro hledání maximálního toku, který jsme si ukazovali na začátku – neposíláme záporné toky jako ve FF
• síť je potřeba dočistit – zbavit se slepých uliček tam, kde jsme smazali hranu
• v síti s iracionálními kapacitami existuje maximální tok
  • Dinic nevyžaduje nic jako racionalitu hran a je schopen vydat maximální tok pro každou síť

Analýza složitosti

• každá fáze trvá $\mathcal{O}(nm)$

  • hledání blokujícího toku je celkově v $\mathcal{O}(nm)$

    • pro každou orientovanou cestu projdeme nejvýše $n$ vrcholů

    • orientovaných cest je nejvýše $m$

      $\implies \mathcal{O}(nm)$

  • sestrojení sítě rezerv, hledání nejkratší cesty, čistění sítě i zlepšování toku trvají $\mathcal{O}(m)$

• proběhne $\mathcal{O}(n)$ fází

  • délka $l$ nejkratší cesty ze $z$ do $s$ vzroste po každé fázi alespoň o 1
  • $R_i$ je síť rezerv v $i$-té fázi poté, co jsme z ní smazali hrany s nulovou rezervou, ale ještě před pročištěním, její nejkratší cesta ze $z$ do $s$ je dlouhá $l$
    • rozdíl $R_{i+1}$ od $R_i$:
      • z každé cesty délky $l$ jsme v síti rezerv smazali alespoň jednu hranu (každá musela být zablokována blokujícím tokem)
        • žádná z původních cest délky $l$ tak v $R_{i+1}$ již neexistuje
  • pokud nějaká hrana měla nulovou rezervu a během fáze jsme zvýšili tok v protisměru, rezerva se zvětšila a objevila se hrana v $R_{i+1}$
    • vzniklá cesta je ale délky $l+2$ – nově vzniklá hrana se nutně vrací zpátky do vrstvy blíž ke zdroji a navazuje na jinou „dopřednou” hranu
  • nejdelší možná cesta mezi $z$ a $s$ je délky $n$

• ve výsledku tedy $\mathcal{O}(n^2m)$

Goldbergův algoritmus

• pro síť vezme tak přemrštěné ohodnocení hran, že to ani není tok a následně tyto hodnoty ořezává, až se z nich tok stane

Vlna

Definice: Funkce $f : E \rightarrow \R^⁺_0$ je vlna v síti $(V,E,z,s,c)$, splňuje-li obě následující podmínky

1. $\forall{e} \in E:f(e) \leq c(e)$ – vlna nepřekročí kapacity hran
2. $\forall{v} \in V \setminus \{z,s\} : f^{\Delta}(v) \geq 0$ – přebytek ve vrcholu je nezáporný
   • mohou mít přebytky, ale nesmí mít deficity

Převedení vlny po hraně $uv$

• zavedeme výšky vrcholů $h(u)$

• když $f^{\Delta}(u) > 0, r(uv) > 0, h(u) > h(v)$ – existuje přebytek ve vrcholu, existuje rezerva na hraně $uv$ a $u$ je výš než $v$

  • tok na hraně $uv$ zvýšíme o $\delta := min \left( r(uv), f^{\Delta}(u) \right)$ – přeliju to co můžu

Definice: převedení je nasycené, když vynuluje rezervu hrany

• nenasycené převedení vynuluje přebytek $f^{\Delta}(u)$

Algoritmus

Poznámky k implementaci

• seznam $S := \text{seznam vrcholů s přebytkem}$
  • údržba $\mathcal{O}(1)$ při změně $f^{\Delta}(v)$
  • výběr v kroku $7$ : $\mathcal{O}(1)$
• $\forall v : K(v) := \{ vu | r(vu) > 0 \and h(u) > h(v) \}$ (seznam klesajících hran $vu$ s kladnou rezervou)
  • převedení po $uv$ je $\mathcal{O}(1)$
  • zvednutí $u$ stojí $\mathcal{O}(n)$
    • to ale nevadí, zvednutí je dle Z $2n^2$ $\rightarrow$ všechna zvednutí trvají $\mathcal{O}(n^3)$

Analýza složitosti

• $\mathcal{O}(n^2m)$

  • všechna zvednutí trvají $\mathcal{O}(n^3)$

  • nasycená převedení trvají $\mathcal{O}(nm)$

  • nenasycená převedení trvají $\mathcal{O}(n^2m)$ – počet hran je vyšší než počet vrcholů, takže tohle je ten bottleneck

Invariant A (základní)

1. $f$ je vlna
2. $\forall v: h(v)$ neklesá
3. $h(z) = n$ a $h(s) = 0$
4. $\forall v \ne z: f^{\Delta}(v) \ge 0$

Invariant S (o spádu)

• $\nexists uv \in E: r(uv) > 0$ $\and$ $h(u) - h(v) > 1$
  • neexistuje hrana s kladnou rezervou (nenasycená hrana) a rozdílem výšek (spádem) větším než 1
    • zvedáme vždy jen o jedna, jakmile je někde spád 1, dochází k převedení – nikdy se nedostaneme do spádu 2

Lemma K (o korektnosti)

• pokud se algoritmus zastaví, $f$ je maximální tok

Důkaz

• algoritmus běží do té doby, dokud existují nějaké přebytky
  • když se algoritmus zastaví, vydá tok
• kdyby tok nebyl maximální, podle FF $\exist P$ nenasycená cesta ze $z$ do $s$
  • cesta překonává spád $n$, ale má nejvýše $n-1$ hran $\implies$ $\exist e \in P \text{ se spádem }\ge 2$
    • spor s invariantem S

Invariant C (o cestě do zdroje)

• $\forall v : f^{\Delta}(v) > 0: \exist P$ nenasycená cesta z $v$ do $z$
  • pro každý vrchol s kladným přebytkem existuje nenasycená cesta do zdroje

Důkaz

• $A := \{ a \in V | \exists \text{nenasycená cesta }v \rightarrow a \}$
  • množina všech vrcholů, do kterých vede nenasycená cesta z $v$ (a $v$ má kladný přebytek)
  • chceme ukázat, že $z \in A$
• $\sum_{a \in A} f^{\Delta}(a) = f(\bar{A}, A) - f(A, \bar{A}) \le 0$
  • všechny hrany vedoucí z $A$ jsou nasycené (jinak by se dal tok zlepšovat)
    • $f(\bar{A}, A) = 0$, čímž pádem musí platit $f(A, \bar{A}) \ge 0$
  • víme ale, že suma obsahuje kladný člen $f^{\Delta}(v)$, bude tedy muset obsahovat i záporný člen
    • jediný vrchol se záporným přebytkem je zdroj $z$

Invariant H (o výšce)

• $\forall h(v) \le 2n$

• zvedneme $v \in V$ z výšky $2n$ tehdy, když $f^{\Delta}(v) > 0$

  • dle C $\exists P$ nenasycená cesta z $v$ do $z$
    • to je dle S spor

Invariant Z (o zvednutí)

• $\#\text{zvednutí} \le 2n^2$
• každý vrchol můžu dle H zvednout jen $2n$-krát

Lemma Sp (o sytých převedeních)

• převedení – převedu po hraně minimum z rezervy hrany a přebytku ve vrcholu

  • pokud převedu rezervu hrany, převedení je nasycené

• $\# \text{nasycených převedení} \le n \cdot m$

  • každou hranu převedu nasyceně maximálně $n$-krát

Důkaz

• uvažme hranu $uv$ s nulovou rezervou ($u$ je o 1 výše než $v$ dle S)
  • $v$ se musí zvednout alespoň 2krát pro obrácení směru $uv$ pro převedení přebytku ve $v$ ($uv$ tím získá rezervu)
  • $u$ se následně musí zvednout alespoň 2krát pro převedení směru zpět z kopce
    • tímto se po každém nasyceném převedení zvětší výška obou vrcholů o 2
• podle H je výška každého vrcholu je nejvýše $2n$ $\rightarrow$ převedení je nejvýše $n$

Lemma Np (o nenasycených převedeních)

• převedení – převedu po hraně minimum z rezervy hrany a přebytku ve vrcholu

  • pokud převedu přebytek ve vrcholu, převedení je nenasycené

• potenciálový argument

Definice: potenciál $\phi := \sum\limits_{\substack{v \in z,s \\ f^{\Delta}(v > 0)}} h(v)$ – součet výšek vrcholů s přebytkem

1. $\phi \ge 0$
2. na počátku $\phi = 0$
3. zvednutí
   • zvýší $\phi$ přesně o 1
   • stane se nejvýše $2n^2$-krát
4. Sp
   • mohlo se stát, že $v$ mělo předtím nulový přebytek, ale nyní jsme ho zvětšili, tedy jeho výška bude započítána do $\phi$
   • mohlo se stát, že $u$ mělo předtím nenulový přebytek, ale nyní jsme ho vynulovali, tedy jeho výška zmizí z $\phi$
     • $\phi$ se zvýšil nejvýše o $2n$
     • všechna nasycená převedení zvýší potenciál maximálně o $2n^2m$
5. Np
   • určitě se vynuluje přebytek $u$, jeho výška z $\phi$ určitě zmizí
   • možná se z nulového přebytku $v$ stane nenulový, tedy jeho výška bude započítána do $\phi$
     • $\phi$ se snížil alespoň o 1

• potenciál celkově stoupne o $\mathcal{O}(n^2m)$ a při nenasycených převedení klesá alespoň o 1
  • všech nenasycených převedení je $\mathcal{O}(n^2m)$

Vylepšení Goldbergova algoritmu

Lemma Np’

• pokud budeme vybírat $v$ s největší výškou $h(v)$ a $f^{\Delta}(v) > 0$, nastane $\mathcal{O}(n^3)$ nenasycených převedení

Důkaz

• $H := max \{ h(v) | f^{\Delta}(v) > 0, v \ne z,s \}$ – maximum ze všech výšek vrcholů s přebytkem

• fáze končí změnou $H$

  • $\# \text{fází} \in \mathcal{O}(n^2)$
    • počet zvýšení je dle H max. $2n^2$
    • počet snížení je shora omezen počtem zvýšení – $2n^2$

• během jedné fáze se každý vrchol účastní maximálně na 1 nenasyceném převedení

  • po každém nenasyceném převedení po hraně $uv$ se vynuluje přebytek v $u$

    • do $u$ už nemůže nic shora přitéct, protože je nejvýše – to zaručuje námi definované vylepšení

  • počet nenasycených převedení ve fázi $\le n$

Rychlá Fourierova transformace

Polynomy

• lze reprezentovat jako vektor: $\vec{P} = (p_0, p_1, ..., p_{n-1})$
• $n$ – velikost polynomu
• $n-1$ – stupeň polynomu
• normalizace: $p_{n-1} \ne 0$ nebo $n=0$ – vyházím počáteční nuly vektorů

Rovnost polynomů

• polynomy jsou identické, pokud mají stejné vektory po normalizaci
  • z toho vyplývá rovnost funkcí – $\forall x : P(x) = Q(x)$
  • toto je ekvivalentní!

Věta: Nechť $P$, $Q$ jsou polynomy stupně max. $d$ a $P(x_j) = Q(x_j)$ pro navzájem různá čísla $x_0$ až $x_d$. Potom $P=Q$.

Lemma: Pro polynom $P$ stupně $d \ge 0$, počet kořenů je nejvýše $d$

Důkaz věty: $R:= P-Q$

• $\forall j : R(x_j) = P({x_j})-Q(x_j)$
• stupeň $R \le d$ a každé z čísel $x_0, \dots, x_d$ (to je $d+1$ hodnot!) je jeho kořenem
  • podle lemmatu $R$ musí být nulový polynom, takže $P = Q$

Násobení

• pro BŮNO stejně velké $P$ a $Q$

• násobení celkem trvá $\mathcal{O}(n^2)$

Graf polynomu

• tentokrát opravdu jen ta křivka

• pevně zvolíme $x_0$ až $x_{n-1}$ navzájem různých

• pomocí nich definujeme polynom velikosti $n$ (a stupně $n-1$) jako vektor funkčních hodnot v těchto bodech

  • toto je jednoznačná reprezentace!

• násobení je nyní triviální – pokud $R = P \cdot Q$, pak $R(x) = P(x) \cdot Q(x)$

• problémky:

  1. násobení polynomů zvětšuje stupěň
     • BÚNO horních $\frac{n}{2}$ koeficientů $P$ a $Q$ jsou nuly (prostě je tam doplníme no)
  2. jak rychle přejít z koeficientů ke grafu?
  3. jak rychle přejít z grafů ke koeficientům?

(Chybné) rychlé vyhodnocování

• polynom $P$ můžeme rozložit na členy se sudými exponenty a na ty s lichými:

• navíc můžeme z druhé závorky vytknout $x$:

• v obou závorkách se nyní vyskytují pouze sudé mocniny $x$, proto můžeme každou z nich chápat jako vyhodnocení nějakého polynomu velikosti $\frac{n}{2}$ v bodě $x^2$:

• pokud do $P$ dosadíme hodnotu $-x$, dostaneme:

• vyhodnocení polynomu $P$ tedy můžeme převést na vyhodnocení polynomů $P_s$ a $P_l$ poloviční velikosti, mohli bychom pak takto pokračovat s dělením velikostí dál
  • problém – druhé mocniny reálných čísel jsou vždy nezáporné, v dalších vrstvách by tedy nebylo možné dělení provést

Intermezzo o komplexních číslech

• různé tvary – algebraický, goniometrický, exponenciální

Algebraický tvar

• $z = a + b\cdot i$ $a,b \in \R$
• $\bar{z} = a - b \cdot i$

Goniometrický tvar

• $z=|z|(\cos{\varphi} + i \cdot \sin{\varphi})$
• číslu $\varphi(z)$ říkáme argument čísla $z$ – ($\text{arg }z$)
• $\varphi(\bar{z}) = - \varphi(z)$

Exponenciální tvar

• z Taylorova rozvoje
• Eulerova formule: $e^{i\varphi} = \cos \varphi + i \cdot \sin \varphi$

Odmocniny z jedničky

• v $\R$ jednoznačné, v $\C$ množina!

• pozorování: násobení komplexní jednotkou otáčíme číslo o $\varphi$

• odmocňování obecně: $\sqrt[n]{z} = {|z|}^{\frac{1}{n}} \cdot e^{i \frac{\varphi(z)}{n}}$

• některé odmocniny jedničky ale vypadaj líp než jiné (komunismus moment?)

Definice: $\omega \in \C$ je primitivní $n$-tá odmocnina z 1 tehdy, když $\omega = 1$ a $\omega ^1$ až $\omega ^{n-1} \ne 1$

• neexistuje menší odmocnina, která by také byla rovna 1

  • body které navštívím při mocnění jsou navzájem různé – můžu si je představit jako rozdělovače na jednotkové kružnici v $\C$

• pro sudé $n$ platí $\omega ^{\frac{n}{2}} = -1$

  • otočím se jen o půlku původního úseku – půlku jednotkové kružnice

FFT

• polynom budeme vyhodnocovat v bodech $\omega^0,\omega^1,\dots,\omega^{n-1}$, kde $\omega$ je nějaká primitivní $n$-tá odmocnina z jedničky
  • hodnoty $\omega^{\frac{n}{2}},\dots,\omega^{n-1}$ se od $\omega^0,\dots,\omega^{\frac{n}{2}-1}$ liší pouze znaménkem
• používáme původní chybný algoritmus rozděl a panuj, ale opravujeme ho komplexními čísly

• $\mathcal{\Theta}(n \log{n})$

  • poslední smyčka od (body 6., 7. 8.) je v $\mathcal{\Theta}(n)$
  • pak máme logaritmicky mnoho rekurzivních volání

• výsledek odpovídá DFT

• Fourierova transformace vektoru $\vec{v}$ lze popsat maticovým násobením:

Inverzní FFT

• maticově: $\Omega \cdot \bar \Omega = n \cdot E$

• tato suma je nulová, pokud $j \ne k$. Pokud $j = k$, tedy jsme na diagonále, suma bude rovna $n$.

• takže pro zpětný chod použiju také fourierku, ale místo $\omega$ použijeme $\bar \omega$ a nakonec vydělíme $n$

Vzorkování periodických funkcí

Věta: Nechť $\vec{x} \in \R^n$ a $\vec{y} = \mathcal{F}(\vec{x})$. Potom $\vec{y}_j = \overline{\vec{y}_{n-j}}$ pro všechna $j$

• tím pádem můžeme každý reálný vektor zapsat jako lineární kombinaci navzorkovaných sinů a cosinů

Paralelní algoritmy

Hradlo

• nějaká krabička, která obsahuje nějakou funkci $f$
• má $k$ vstupů (hradlo je arity $k$) a jeden výstup
  • $f: \Sigma^k \rightarrow \Sigma$
  • $\Sigma$ – konečná abeceda, typicky $\left\{ 0, 1 \right\}$

Boolovská hradla

• arita 2 (binární) – AND, OR, XOR, $\le$
• arita 1 (unární) – NOT
• arita 0 (konstanty) – 0, 1

Hradlové sítě

• zpracovává jen konkrétní velikost vstupu (oproti běžnému výpočetnímu modelu)
• pro zpracování různých velikostí vstupů máme posloupnost různých hradlových sítí
  • neuniformní

Majorita

• $maj(x, y, z)$ vrátí „většinový názor” – je víc nul či jedniček

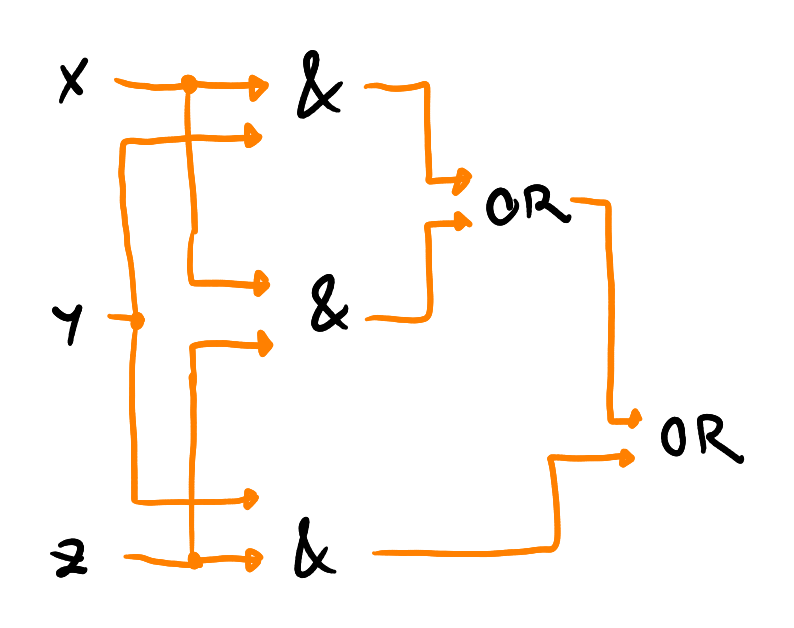
Složení hradlových sítí

• hradla
• vstupní porty
• výstupní porty
• acyklická propojení

Průběh výpočtu

• nultý takt – vyhodnotíme vstupní porty a konstanty

• i + 1. takt – ohodnotíme hradla a porty, jejichž vstupy byly ohodnoceny nejpozději v i. taktu

• to nám síť rozděluje na pomyslné vrstvy

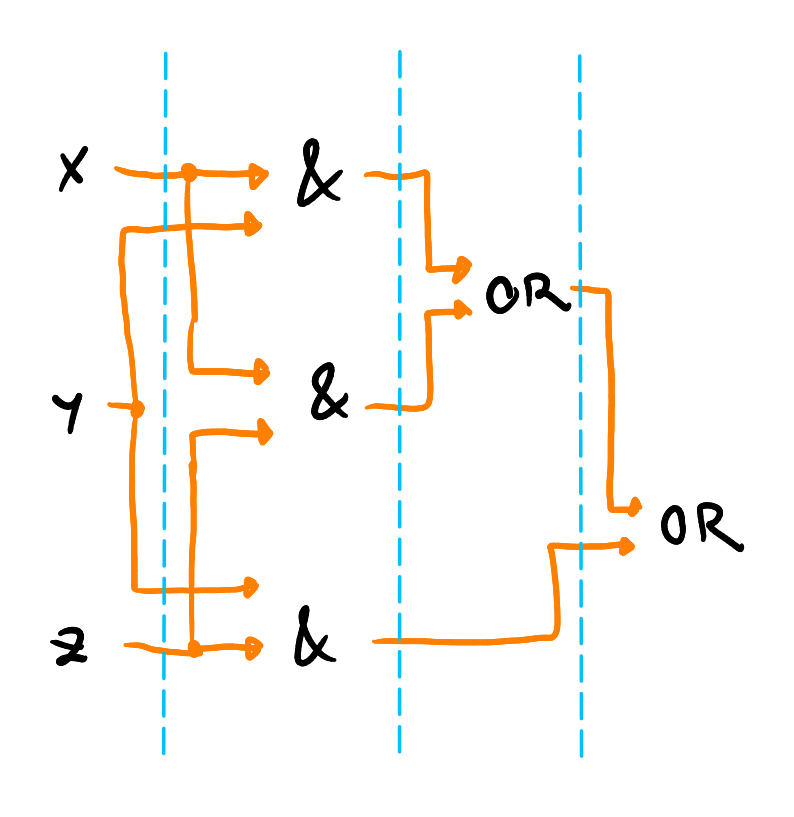
• čas = počet vrstev
• prostor = počet hradel
  • musíme omezit aritu nějakou konstantou – jinak bychom mohli definovat hradlo, které řeší obecné problémy v konstantním čase, což je trochu švindl

Posloupnosti hradlových sítí

• $\text{OR}(x_1, x_2, \dots, x_n)$

• $\mathcal{O}(n)$

• $\mathcal{O}(\log{n})$

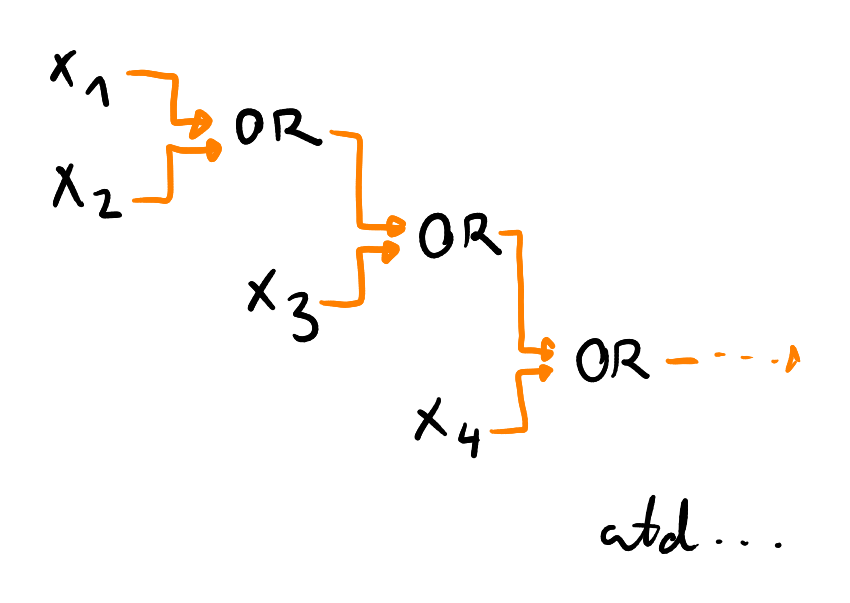
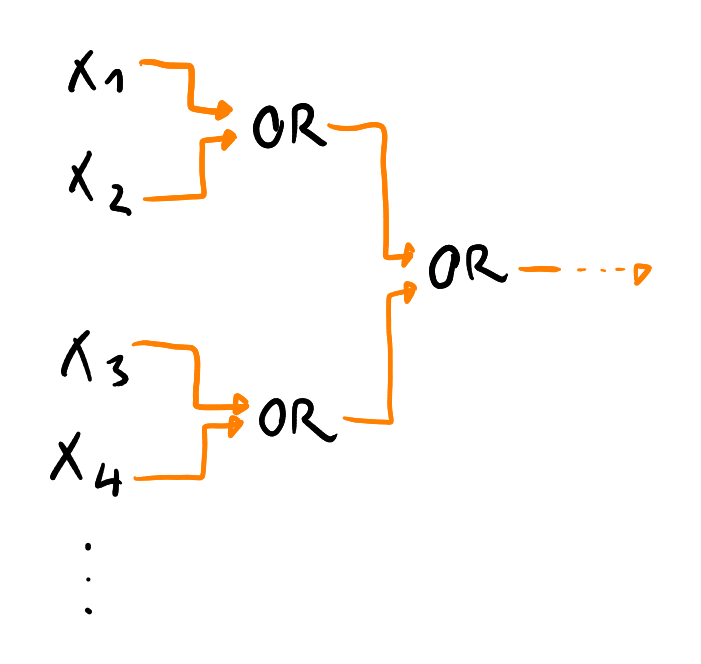
Sčítání

• při běžném sčítání nás brzdí čekání na přenosy z nižších řádů

  • jak budou vypadat jednotlivá chování jednobitových bloků?
    • (1,1) = 1 – přenos určitě nastane
    • (0,0) = 0 – přenos určitě nenastane
    • (1,0) = < – přenos nastane jen tehdy, když nastal přenos předtím

  

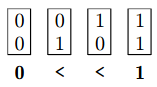
  • jak bude vypadat chování kanonických bloků?
    • (0,*) = 0 – pokud horní polovina pohlcuje, celý blok pohlcuje
    • (1,*) = 1 – pokud horní polovina přenáší, celý blok přenáší
    • (<,0) = 0 – horní polovina kopíruje to, co do ní přijde z dolní poloviny
    • (<,1) = 1
    • (<,<) = <

• algoritmus rozdělíme na části:

  1. spočítáme chování všech kanonických bloků
     • nejdříve stanovíme chování bloků velikosti 1, pak velikosti 2, 4, 8, …
     • $\mathcal{O}(\log{n})$
  2. dopočítáme přenosy
     • v $i$-tém kroku budou známy přenosy do řádů dělitelných $2^{\log{n}-i}$
  3. paralelně sečtu a přičtu přenosy

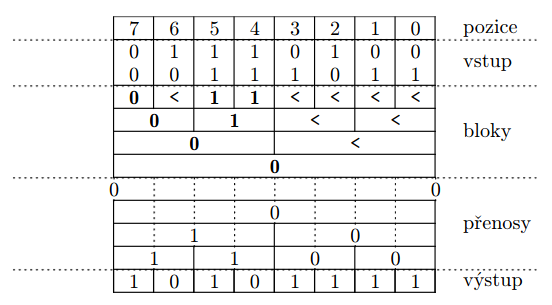
Násobení

• násobení dvou $n$-ciferných binárních čísel $x$ a $y$:

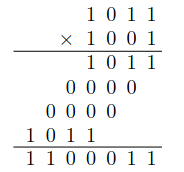
• v binárce je násobení jednou číslicí AND
  • paralelně tedy vytvoříme všechna posunutí a jejich ANDy
  • zbývalo by sečíst $n$ $n$-bitových čísel – $\mathcal{O}(log^2{n})$

Kompresor

• vstup: 3 čísla $x$, $y$ a $z$, výstup: 2 čísla $p$ a $q$
• pro každý řád $i$ spočteme součet $x_i + y_i + z_i$ – dvoubitové číslo
  • $p_i$ = nižší bit tohoto čísla
  • $q_{i+1}$ = vyšší bit tohoto čísla

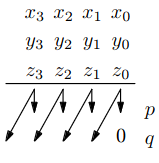
• konstantní!
• máme-li sečíst $n$ čísel, v konstantním čase převedeme úkol na sečtení $\frac{2}{3}n$ čísel
  • dovolí sčítání $n$ $n$-bitových čísel v hloubce $\mathcal{O}(\log{n})$

Třídění

Komparátorová síť

• hradlová síť složená z komparátorů
• vstup – 2 čísla
• výstup – vlevo menší číslo, vpravo větší číslo

Bubble sort

• čas $\Theta(n)$

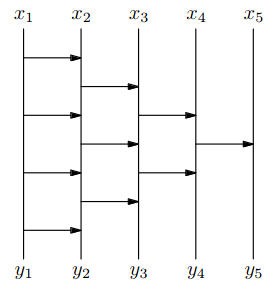
Bitonické třídění

Definice: Posloupnost $x_0,\dots,x_{n-1}$ je čistě bitonická, pokud ji můžeme rozdělit na nějaké pozici $k$ na rostoucí posloupnost $x_0,\dots,x_k$ a klesající posloupnost $x_k,\dots,x_{n-1}$.

Definice: Posloupnost je bitonická, jestliže ji lze získat rotací nějaké čistě bitonické posloupnosti

Separátor

• rozdělí bitonickou posloupnost na dvě poloviční a navíc jsou všechny prvky v první polovině menší než všechny v té druhé.
• pro $i=0,\dots,\frac{n}{2}-1$ zapojíme komparátor se vstupy $x_i$ a $x_{i+\frac{n}{2}}$
  • minimum přivedeme na $y_i$ a maximum na $y_{i + \frac{n}{2}}$

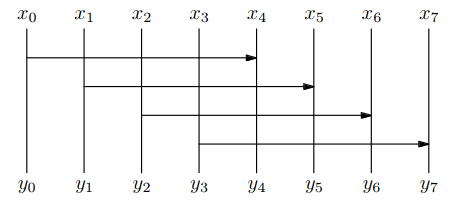
• separátor má zřejmě hloubku 1 a využívá $n$ hradel

Důkaz správnosti

• cancerrrrrr

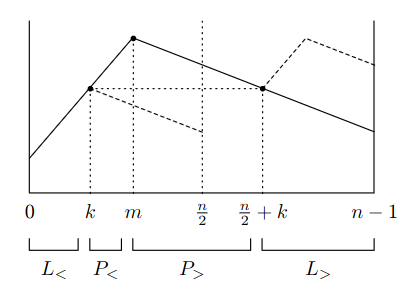
• nejdříve předpokládejme, že vstupem je čistě bitonická posloupnost

• maximum BÚNO leží v první polovině na indexu $m$ (kdyby ne, bude důkaz zrcadlově)

• nechť $k$ je nejmenší index, pro který komparátor hodnoty $x_k$ a $x_{\frac{n}{2}+k}$ prohodí

• maximum je jedinečné, $k$ tedy určitě existuje a platí $0 \le k \le m < \frac{n}{2}$

• pro $i = k,\dots,\frac{n}{2}-1$ komparátory vždy prohazují

  • pro $i \ge m$ je vidět přímo, pro $i < m$ je $x_i \ge x_k > x_{\frac{n}{2}+k}$

• levá polovina vznikne slepením rostoucího úseku $x_0,\dots,x_{k-1}$ s klesajícím úsekem $x_{\frac{n}{2} + k},\dots,x_{n-1}$

• pravá polovina vznikne slepením klesajícího úseku $x_{\frac{n}{2}},\dots,x_{\frac{n}{2}+k-1}$, rostoucího úseku $x_k,\dots,x_{m-1}$ a klesajícího úseku $x_m,\dots,x_{\frac{n}{2}-1}$

• obě poloviny jsou bitonické

• levá polovina je menší než pravá

  • rozdělíme levou polovinu na rostoucí část $L_<=x_0,\dots,x_{k-1}$ a klesající část $L_>=x_{\frac{n}{2}+k},\dots,x_{n-1}$
  • rozdělíme pravou polovinu na rostoucí část $P<=x_k,\dots,x_{m-1}$ a $P_>=x_m,\dots,x_{\frac{n}{2}+k-1}$
  • $L_< < P_<$ – obě části původně tvořily rostoucí úsek $L_
  • $L_< < P_>$ – nejvyšší prvek z $L_<$ je menší než nejnižší prvek z $P_>$ – jinak bychom mohli snížit $k$
  • $L_> < P_<$ – nejvyšší prvek z $L_>$ je menší než nejnižší prvek z $P_<$
  • $L_> < P_>$ – obě části původně tvořily jeden společný klesající úsek $P_>L_>$

• pokud by vstup nebyl čistě bitonický

  • separátor je symetrický: zrotujeme-li jeho vstup o $p$ pozic, dostaneme o $p$ pozic zrotované i obě poloviny výstupu
  • pro nečistou bitonickou posloupnost tedy separátor vydá akorát zrotovaný výsledek, což nám nevadí

Bitonická třídička

• nejprve separátorem $S_n$ zadanou bitonickou posloupnost rozdělíme na dvě bitonické posloupnosti délky $\frac{n}{2}$, každou z nich pak separátorem $S_{\frac{n}{2}}$ rozdělíme na dvě části délky $\frac{n}{4}$, atd. atd., až získáme jednoprvkové posloupnosti ve správném pořadí

• $\log{n}$ hladin s $n\log{n}$ komparátory

Bitonická slévačka

• na vstupu dostane dvě setříděné posloupnost délky $n$, vydá setříděnou posloupnost vzniklou jejich slitím
• stačí první posloupnost obrátit, přilepit za tu druhou a setřídit bitonickou třídičkou $B_{2n}$
• hloubka $\log{n}$ s $n\log{n}$ komparátory (bottleneck je třídička)

Třídící síť

• inspirace v Mergesortu

• vstup rozdělíme na $n$ jednoprvkových posloupností, které postupně slévačkami sléváme dohromady

• celkem provedeme $\log{n}$ kroků slévání, $i$-tý z nich obsahuje slévačky hloubky $\Theta(i)$

  • celková hloubka je tak $\Theta(1+2+3+\dots+\log{n}) = \Theta(\log^2{n})$
  • každý krok potřebuje $\Theta(n\log{n})$ komparátorů, což dává $\Theta(n\log^2{n})$ komparátorů

Geometrické algoritmy

Konvexní obal

• máme danou množinu $n$ bodů, snažíme se nalézt nejkratší uzavřenou křivku, uvnitř níž jsou všechny zadané body

• konvexní obal je posloupnost bodů

• pro malé počty bodů:

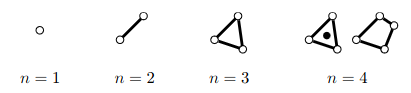
• předpoklady:

  • všechny body mají navzájem různé $x$-ové souřadnice
    • toho můžeme v reálu docílit tím, že si rovinu myšlenkově otočíme o velmi malé $\epsilon$ po směru hodinových ručiček
    • množiny bodů, které měly předtím stejnou $x$-ovou souřadnici se nám nyní uspořádají vzestupně dle jejich $y$-souřadnice
  • konvexní obal se skládá z horní a spodní „obálky”
    • horní obálka je striktně konkávní, dolní konvexní
    • konvexní obal je horní obálka + obrácená dolní obálka

• budeme zametat rovinu zleva doprava a udržovat si horní a dolní obálku

Orientace úhlu

• pro každý nový bod potřebujeme zjistit, jestli patří do horní, nebo dolní obálky

• pomocí $\sin$ a $\cos$

  • v praxi pomalé a nepřesné

• pomocí determinantu

  • znaménko determinantu určuje orientaci vektorů

  • pokud jsou navíc hodnoty souřadnic bodů celočíselné, i determinant je celočíselný

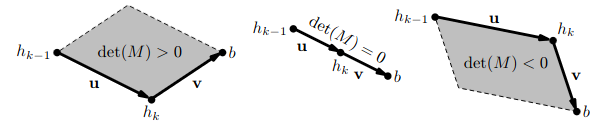
Analýza složitosti

• třídění zadaných bodů – $\mathcal{O}(n\log{n})$

• přidání dalšího bodu do obálek je lineární vzhledem k počtu odebraných bodů

  • každý bod je ale odebrán nejvýše jednou – přidání je amort. $\mathcal{O}(1)$
  • všechna přidání jsou celkem $\mathcal{O}(n)$

• celkem: $\mathcal{O}(n\log{n})$

Průsečíky úseček

• $n$ úseček

• hledáme všechny průsečíky

  • těch může být až $n^2$, a tak by algoritmus hrubou silou měl být optimální, ne? WRONG!

• předpoklady:

  • žádné tři úsečky se neprotínají v jednom bodě
  • průnikem dvou úseček je nejvýše jeden bod
  • krajní bod úsečky neleží na žádné jiné úsečce
  • neexistují vodorovné úsečky

• budeme zametat rovinu odshora dolů

  • neprocházíme celou rovinu, zastavujeme se jen na zajímavých místech – událostech

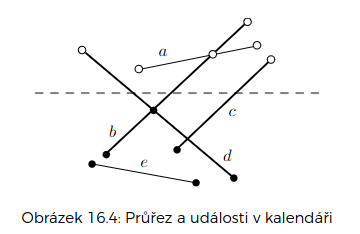
• událost – začátek, konec či průsečík úseček

• průřez – množina úseček proťatých zametací přímkou (seřazen zleva doprava)

  • pokud si budeme průsečíků všímat jen tehdy, kdy protínající úsečky sousedí v průřezu, nikdy žádný průsečík nemineme

• kalendář – naplánované začátky, konce a průsečíky pod zametací přímkou

  • začátky a konce úseček můžeme přidat všechny hned na začátku
  • průsečíky přidáváme do kalendáře tehdy, když se dvě sousední úsečky v průřezu protínají
  • průsečíky odstraňujeme z kalendáře tehdy, když odpovídající dvě úsečky v průřezu přestanou sousedit – jinak bychom mohli několik průsečíků přidat víckrát

Reprezentace

• Kalendář
  • halda nebo BVS
    • $\mathcal{O}(n)$ událostí
    • $\mathcal{O}(\log{n})$ času na operaci
• Průřez
  • potřebujeme vkládat a odebírat úsečky, hledat nejbližší další úsečku vlevo či vpravo od aktuální
  • vyvažovaný BVS s úsečkami jako klíči
    • úsečka $a$ je nalevo od $b$ tehdy, když je její průsečík se zametací přímkou více vlevo
      • to trochu suckuje, to bych musela přepočítávat furt znova a znova
      • úsečka $a$ je nalevo od $b$ tehdy, když začátek $a$ je nalevo od začátku $b$ a jejich průsečík není nad zametací přímkou
        • pokud je jejich průsečík nad zametací přímkou, $a$ je napravo od $b$ – to ošetřujeme prohazováním v $P$
    • $\mathcal{O}(n)$ úseček
    • $\mathcal{O}(\log{n})$ času na operaci

Analýza složitosti

• počet událostí je $2n + p$
• na jednu událost máme konstantní počet operací s datovými strukturami
  • jednu událost zpracujeme v čase $\mathcal{O}(\log{n})$
• celý algoritmus provedeme v čase $\mathcal{O}((n+p)\log{n})$ a paměti $\mathcal{O}(n)$
  • existuje algoritmus, který to zvládá v čase $\mathcal{O}(n\log{n} + p)$

Voroného diagramy

• pro množinu míst $x_1, \dots, x_n \in \R^2$ je systém oblastí $B_1, \dots, B_n \sube \R^2$, kde $B_i$ obsahuje ty body roviny, jejichž vzdálenost od $x_i$ je menší nebo rovna vzdálenostem od všech ostatních $x_j$.

• 2 body – rovina dělená přímkou

• 3 body – trojmezí

• 4 body – to už vypadá docela složitě

• 5 bodů – oh no…

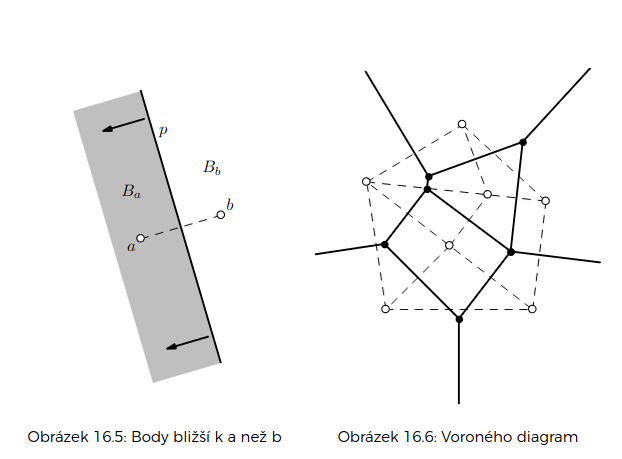
• Voroného diagram je rozklad rodiny na konvexní mnohoúhelníky, kde některé jsou otevřeny do nekonečna

• diagram připomíná rovinný graf (jen stěny nemusí být omezené)

  • vrcholy – body, které jsou stejně vzdálené od alespoň tří zadaných míst ($n$-mezí)
  • stěny – oblastí $B_i$
  • hrany části hranice mezi dvěma oblastmi

Lokalizace bodu

• pokud už máme vybudovaný diagram, jak pro zadaný bod zjistit, do které množiny patří?

• zametáme rovinu odshora dolů

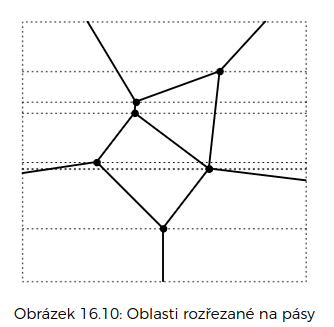
  • udržujeme si průřez hranic oblastí (podobně jako při hledání průsečíků úseček)
    • ten se mění jen při průchodu vrcholy diagramu
    • vlastně jsme rozřezali rovinu na pásy, mezi kterými už jsou jen množiny úseček
  • když při zametání narazíme na bod, který se snažíme lokalizovat, podíváme se, do kterého intervalu mezi hranicemi průřezu patří

Analýza složitosti

• kalendář i průřez máme opět ve stromech – $\mathcal{O}(\log{n})$ na dotaz
  • hledání jednoho bodu – $\mathcal{O}(n\log{n})$
• celkově pro $k$ dotazů: $\mathcal{O}(k\cdot n\log{n})$
  • au au au :(

Předvýpočet

• předpočítáme si rozdělení roviny na pásy

  • pro každý pás známe hranice a průřez (ten je pro každou polohu zametací přímky v pásu stejný)

• nyní stačí pro každý bod najít odpovídající pás a jeho polohu v odpovídajícím průřezu

• problém: pamatovat si pro každý pás separátní průřez zabírá moc místa – $\Theta(n^2)$ – a je tedy i pomalé

Persistentní vyhledávací stromy

• nebudeme průřezy kopírovat, jen si pamatovat jejich „diff”

• každá verze má svůj unikátní identifikátor

• vezmeme obyčejný AVL strom

  • pro novou verzi si zkopírujeme vrchol, který se mění a změníme ho
  • musíme změnit ukazatele z jeho otce (a tím ho změnit)
    • postupně se dostaneme s každou změnou až do kořene, který se stane identifikátorem verze

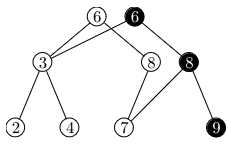
• strom předpočítáme v čase $\mathcal{O}(n\log{n})$ a zabírá $\mathcal{O}(n\log{n})$ paměti

• lokalizace $k$ bodů probíhá v čase $\mathcal{O}(k\log{n})$

Těžké problémy

Rozhodovací problém

• funkce z $\{0, 1\}^* \rightarrow \{0,1\}$ – ze všech možných řetězců 0 a 1 na množinu $\{0, 1\}$
  • zadání každého problému lze zakódovat
• ptám se, jestli něco lze, existuje, …

Bipartitní párování

• je dán bipartitní graf $B$ a číslo $k \in \N$

• máme odpovědět, zda v zadaném grafu existuje párování, které obsahuje alespoň $k$ hran

• jak zakódovat vstup do jedniček a nul?

  

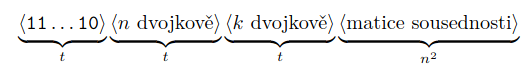
  • počet jedniček na začátku kódu nám řekne, v kolika bitech je uložené $n$ a $k$ a zbytek kódu přečteme jako matici sousednosti
  • na všechny nevalidně utvořené vstupy budeme odpovídat False

• problém lze převést na toky – existuje tok velikosti alespoň $k$?

Převádění

Definice: Jsou-li $A$, $B$ rozhodovací problémy, říkáme, že $A$ lze převést na $B$ (značíme $A \rightarrow B$) právě tehdy, když existuje funkce $f: \{0, 1 \}^* \rightarrow \{0, 1 \}^*$ taková, že pro všechna $x \in \{0, 1 \}^*$ platí $A(x) = B(f(x))$, a navíc lze funkci $f$ spočítat v čase polynomiálním vzhledem k $|x|$. Funkci $f$ říkáme převod nebo také redukce.

Lemma: Nechť $A \rightarrow B$ a $B$ je řešitelné v polynomiálním čase, pak $A$ je řešitelné v polynomiálním čase

• mějme algoritmus řešící $B$ v čase $\mathcal{O}(b^k)$ ($b$ je délka vstupu a $k$ konstanta)
• mějme převod $f$ z $A$ na $B$ v čase $\mathcal{O}(a^l)$ pro vstup délky $a$
• chceme spočítat $A(x)$ pro nějaký vstup $x$ délky $a$
  • nejdříve spočítáme $f(x)$ v čase $\mathcal{O}(a^l)$ – vyjde výstup délky $\mathcal{O}(a^l)$ (delší bychom nestihli vypsat)
  • tento vstup pak předáme algoritmu řešící $B$, který nad ním stráví čas $\mathcal{O}(a^{kl})$
    • celkový čas výpočtu proto činí $\mathcal{O}(a^l + a^{kl})$, což je polynom v délce původního vstupu $\square$

Převoditelnost jako relace

• částečné kvaziuspořádání

  • reflexivní – umím převést problém sám na sebe

  • tranzitivní – pokud umím $A$ převést na $B$ a $B$ na $C$, určitě umím převést $A$ na $C$

  • není symetrická – neumím funkci, která vrací vždy true převést na funkci, která vrací vždy false

  • není antisymetrická – umím převést párování na toky

• některé třídy jsou ekvivalentní a mezi různými třídami je uspořádání

SAT

• satisfiability

  • splnitelnost booleovských proměnných

• klauzule – závorky

• literály – proměnné

• je mnoho SAT-solverů, které jsou v praxi docela rychlé

  • většina NP-problémů se tak převádí na SAT

CNF

• uvnitř klauzulí je libovolně mnoho literálů, mezi kterými je disjunkce, mezi klauzulemi je konjunkce
• existuje dosazení za proměnné takové, že formule je pravdivá? – splňující ohodnocení

3-SAT

• všechny klauzule mají nejvýše 3 literály

• 3-SAT $\rightarrow$ SAT je triviální

• SAT $\rightarrow$ 3-SAT už je zajímavější

SAT $\rightarrow$ 3-SAT

• dlouhou klauzuli lze rozštípnout ve dvě

• pokud bylo $\alpha$ true, splňuje první klauzuli a $\chi$ může být klidně false, takže $\neg \chi$ pak splňuje druhou klauzuli

• podobně pro $\beta$ true

• pokud je délka původní klauzule $l \ge 4$, odeberu z klauzule 2 literály, vytvořím pro ně klauzuli a připojím je za původní klauzuli pomocí nějakého nového $\chi$

• tím jsme délku původní klauzule zmenšili o 1

3,3-SAT

• navíc oproti 3-SATu se každá proměnná vyskytuje nejvýše ve 3 klauzulích

3-SAT $\rightarrow$ 3,3-SAT

• nechť $x$ je proměnná s $k > 3$ výskyty
• rozštípu $x$ na nové proměnné $x_1,x_2,\dots,x_k$ a zařídím, aby všechny měly stejnou hodnotu
  • klauzule $x_1\implies x_2 \implies x_3 \implies \dots \implies x_k \implies x_1$
  • lze převést do CNF – $(a \implies b) \iff (\neg a \or b)$
• dokonce umíme takto zařídit, že každý literál je použit nejvýše 2krát

Nezávislá množina

• hledáme v neorientovaném grafu $G$ množinu vrcholů velikosti $k$, kde mezi vybranými vrcholy nevede žádná hrana

3-SAT $\rightarrow$ NzMna

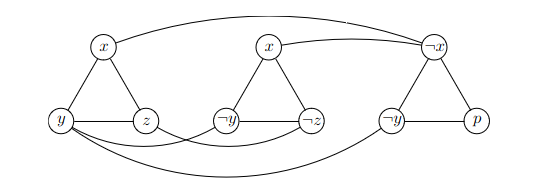
• klauzule $\rightarrow$ trojúhelníky

  • z každého trojúhelníku můžeme pro NM vybrat pokaždé jen jeden vrchol

• hrany mezi $x$ a $\neg x$

  • může zároveň platit jenom jedno

• ohodnocení 3-SATu je splňující tehdy, když je každá klauzule pravdivá

  $\implies$ NzMna velikosti $\ge k = \#\text{klauzulí}$

NzMna $\rightarrow$ SAT

• nechť vrcholy grafu jsou očíslovány 1 až $n$ – $V(G) = \{ 1,2,\dots,n \}$

• pro každý vrchol si pořídíme proměnnou, která říká, jestli jsme daný vrchol vybrali do NzMna – $x_1, x_2, \dots, x_n$

• pro každou hranu $ij$ grafu potřebujeme klauzuli, která zakáže, aby $x_i$ i $x_j$ byly zároveň true

  • klauzule $(\neg v_i \or \neg v_j)$ – alespoň jeden z vrcholů musí být nevybrán

• potřebujeme ošetřit $k$

  • vytvoříme nějaké očíslování vrcholů nezávislé množiny
  • tabulka s $k$ řádky a $n$ sloupci
    • $y_{ij} = \begin{cases}1 : \text{vrchol } j\text{ je } i\text{-tým v NzMna} \\ 0: \text{ostatní} \end{cases}$
      • $y_{ij} \implies x_j$, což lze zapsat pomocí CNF jako $(\neg y_{ij} \or x_j)$
  • v žádném sloupci nechceme 2 true – $\forall i, i', j: (\neg y_{ij} \or \neg y_{i'j})$, kde $i$ a $i'$ jsou různé indexy řádků
  • v žádném řádku nechceme 2 true – $\forall i, j, j': (\neg y_{ij} \or \neg y_{ij'})$, kde $j$ a $j'$ jsou různé indexy sloupců
  • v každém řádku máme alespoň 1 true – $\forall i: (x_{i,1} \or x_{i,2} \or \dots \or x_{i,n})$

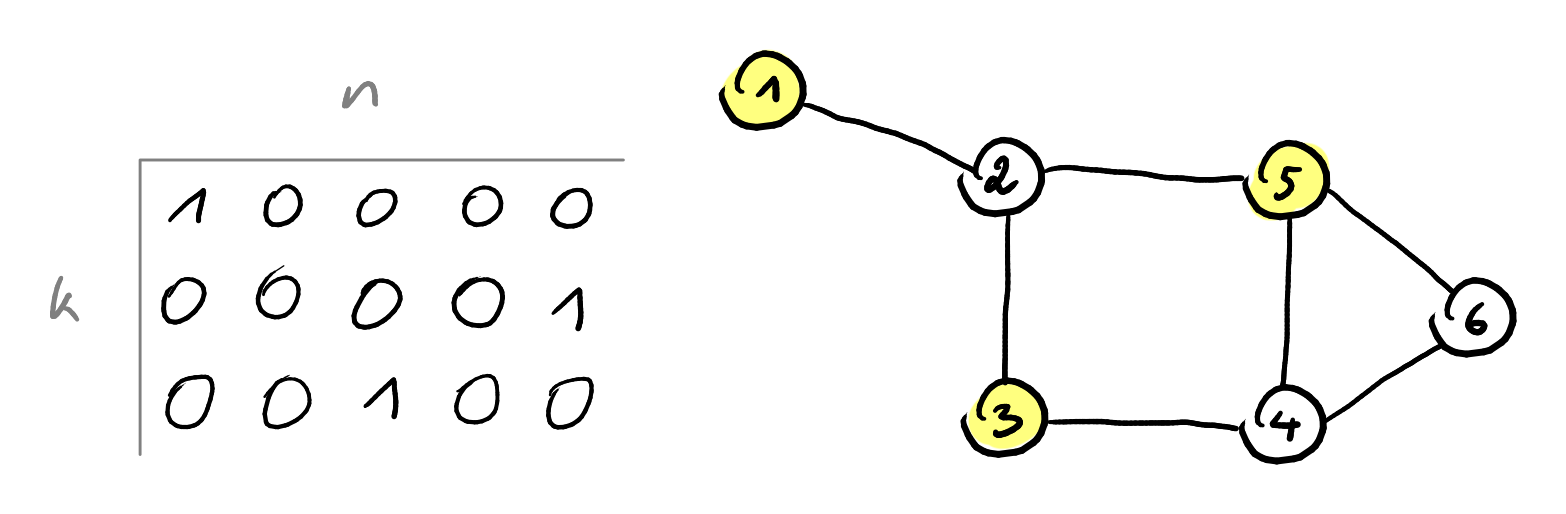
• převod probíhá v polynomiálním čase – vytvoříme polynomiálně mnoho klauzulí a každou z nich stihneme vypsat v lineárním čase

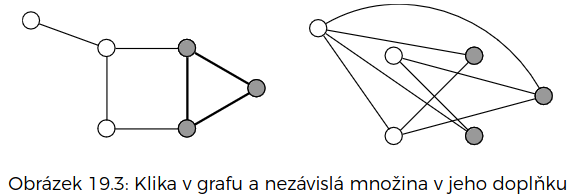
Klika

• hledáme v neorientovaném grafu $G$ množinu vrcholů velikosti $k$, kde mezi každou vybranou dvojicí vrcholů vede hrana
• to je taková opačná NzMna – počítáme na hranovém doplňku grafu

3D-párování

• 3-partitní přiřazení (???)

• 3 množiny $K$, $D$, $Z$ a množina $T \subseteq K \times D \times Z$

  • taký grafík no

• snažíme se najít množinu trojic takovou, že každý prvek $K$, $D$, $Z$ je právě v 1 trojici

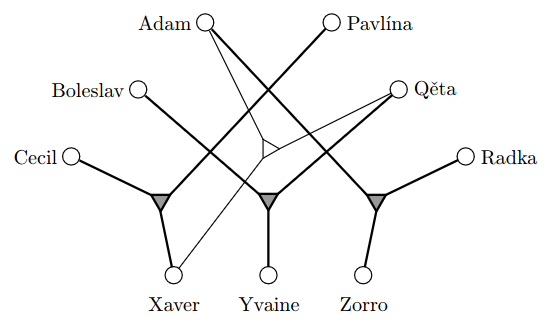
• možná trojice je zakreslená takovým tím trojúhelníčkem s fousy vedoucími k prvkům v trojici
  • tmavý trojúhelníček značí trojici, kterou jsme vybrali do výsledné množiny

3,3-SAT $\rightarrow$ 3D-párování

• pokud chceme SAT převádět na jiný problém, potřebujeme obvykle dvě věci:
  • konstrukci simulující proměnné – nabývá stavů True a False
  • konstrukci simulující klauzule – splnitelné alespoň jednou proměnnou

Gadget pro proměnnou

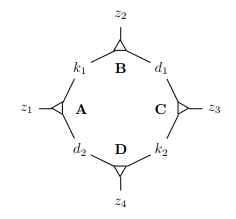
• 2 kluci, 2 děvčata a 4 zvířátka

  • kluci a děvčata hrají roli jen v tomto gadgetu, zvířátka jsou i v ostatních

• $k_1$ musí být v nějaké trojici – $A$, $B$

  • $A \implies$ spárování $k_1$ a $d_2$, takže si nesmíme vybrat $B$ ani $D$
  • pro spárování $k_2$ a $d_1$ musíme vybrat $C$

• vždy si musíme vybrat dvě protější trojice v obrázku a druhé dvě nechat nevyužité

  • binární – vhodné na reprezentaci proměnných
  • $0 := A+ C$ – nespáruje zvířátka $z_2$ a $z_4$
  • $1:= B + D$ – nespáruje zvířátka $z_1$ a $z_3$

Gadget pro klauzuli

• klauzule tvaru $(x \or y \or \neg{r})$
  • potřebujeme zajistit, aby $x$ nebo $y$ bylo 1 nebo $r$ 0

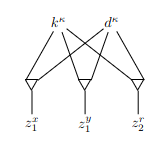
• nová dvojice kluk a dívka – 3 trojice se 3 zvířátky
  • zvířátka z gadgetů pro příslušné proměnné
    • $z_1^x$ – zvířátko z Gadgetu pro pozitivní literál $x$ (můžeme i $z_3^x$, pokud jsme jej nepoužili v jiné klauzuli)
    • $z_2^r$ – zvířátko z Gadgetu pro negativní literál $r$ (má před sebou negaci, žeo)
  • nějaká zvířátka zbudou :(
    • $\#\text{zbylých zvířátek} = 2 \cdot \#\text{proměnných} - \#\text{klauzulí}$
      • 2 zvířátka jsou SATnuta by default zvolením True/False na gadgetu pro proměnnou
      • 1 zvířátko je vždy SATnuto výběrem trojice z gadgetu pro klauzuli
    • přidáme $\#\text{zbylých zvířátek}$ párů kluk a dívka a pro ně trojice s úplně všemi zvířátky
      • i s těmi, co jsou někam zapojená už, prostě úplně úplně úplně se všemi
  • zvířátka nedojdou – proměnná se v klauzulích vyskytuje nanejvýš 2krát pozitivně a 2krát negativně
    • kdyby se vyskytovala 3krát se stejnou hodnotou, pak je ohodnocení těchto klauzulí triviální a můžeme je trashnout

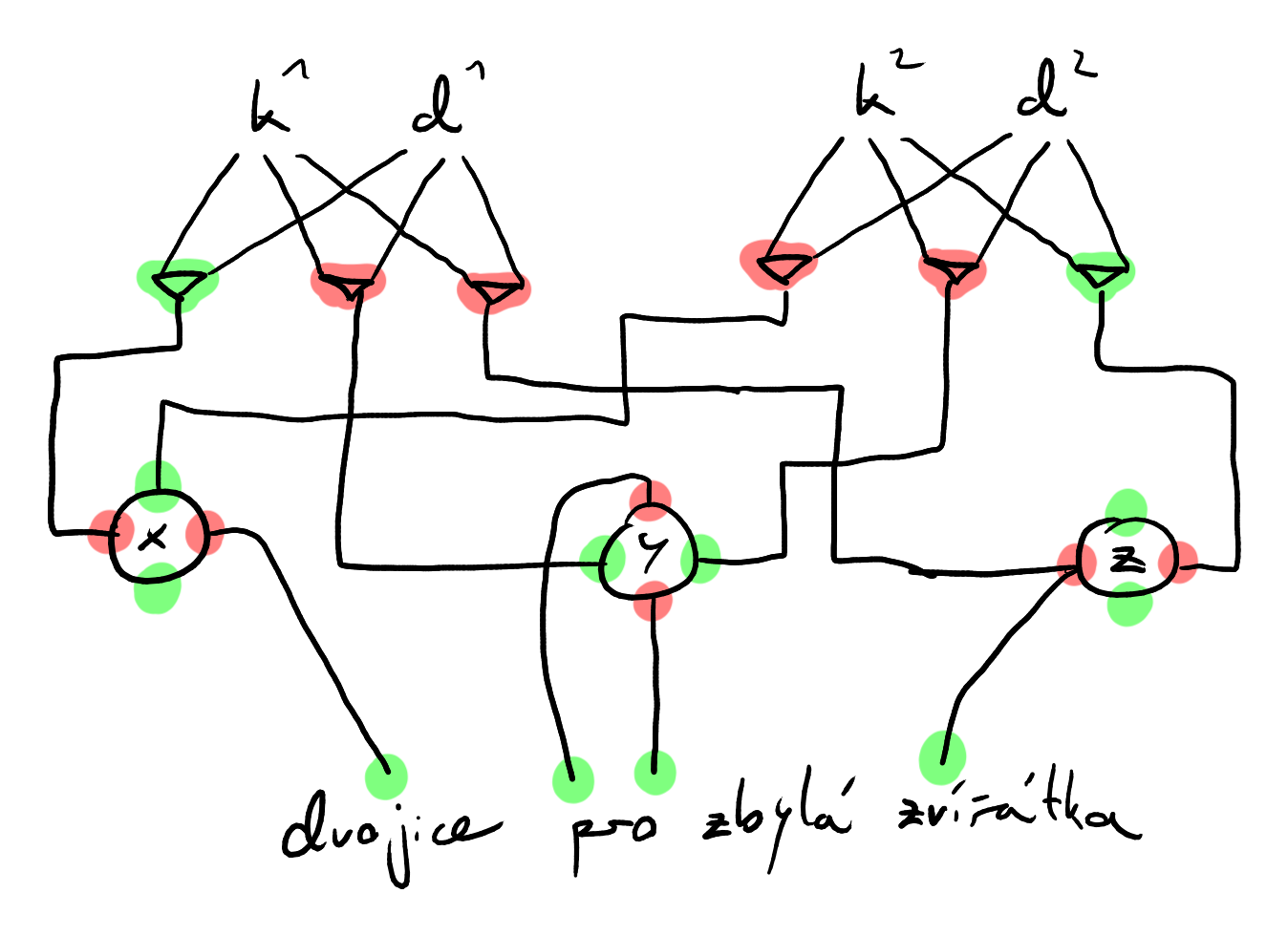
• zapojení pro výrok $(x \or y \or z) \and (\neg x \or y \or z)$
  • zeleně jsou označeny trojice, které jsme vybrali, červeně ty, které jsme nevybrali
  • do dvojice pro zbylá zvířátka ve skutečnosti vede daleko více hran, jen tam nejsou nakreslené
  • $x$ a $z$ jsou True, $y$ je False

Složitostní třídy

Třída P

Definice: Problém $L$ leží v $\text{P}$ tehdy, když existuje nějaký algoritmus $A$ a polynom $f$, přičemž pro každý vstup $x$ algoritmus $A$ doběhne v čase nejvýše $f(|x|)$ a vydá výsledek $A(x)=L(x)$

Třída NP

Definice: $\text{NP}$ je třída rozhodovacích problémů, v níž problém $L$ leží tehdy, když existuje nějaký problém $K \in \text{P}$ a polynom $g$, přičemž pro každý vstup $x$ je $L(x) = 1$ právě tehdy, když pro nějaký řetězec $y$ délky nejvýše $g(|x|)$ platí $K(x,y) = 1$

• Algoritmus $K$ řeší problém $L$, ale kromě vstupu $x$ má i nápovědu $y$ (např. splňující ohodnocení SATu)
• pokud $L(x)=1$, pak $\exists y$, kterou by $K$ schválilo
• pokud $L(x) = 0$, pak $\nexists y$, kterou by $K$ schválilo

• alternativní definice: nedeterministicky polynomiální

  • deterministický – všechno je důsledkem předem daných událostí, takto fungují všechny naše stroje

  • nedeterministický – můj program se může chovat náhodně a nějaká větev výpočtu se dobere výsledku, neumíme simulovat

NP certifikáty

• řetězec $y$ je certifikát stvrzující kladnou odpověď – třeba seznam proměnných se splňujícím ohodnocením pro SAT

  • o negativní odpovědi nevíme vůbec nic (ty říkají něco o problémech v $\text{Co-NP}$)

• polynomiální algoritmus $K$ má za úkol certifikáty kontrolovat

NP-hard

Definice: Problém $L$ je $\text{NP}$-těžký tehdy, když každý problém $K \in \text{NP}$, lze převést na $L$

NP-complete

Definice: Problém $L$ je $\text{NP}$-úplný tehdy, když je $\text{NP}$-těžký a navíc $L\in\text{NP}$

Lemma: pokud $L \in \text{P}$ je $\text{NP}$-těžký, pak $\text{P}=\text{NP}$

• nechť $K \in \text{NP}$

• $K \rightarrow N$ (díky $\text{NP}$-těžkosti)

• $\implies K \in \text{P}$ … proto $\text{NP} \supseteq \text{P}

• logické

  • SAT
  • 3-SAT
  • 3,3-SAT
  • obvodový SAT (pro hradlové sítě)

• grafové

  • nezávislá množina
  • klika
  • vertex cover
  • k-obarvitelnost
  • hamiltonovské cesty a kružnice
  • 3D-párování

• číselné

  • součet podmnožin
    • hledáme podmnožinu přirozených čísel, která se sečte na zadané číslo
  • problém batohu
  • 2 loupežníci
    • jde množina rozdělit na 2 podmnožiny tak, aby měly stejnou cenu?
  • nula jedničkové lineární rovnice
    • hledáme řešení, které obsahuje jen nuly a jedničky
    • stále počítáme v $\R$!

Cook-Levinova věta

Věta: SAT je $\text{NP}$-úplný

Lemma: Nechť $L$ je problém ležící v $P$. Potom existuje polynom $p$ a algoritmus, který pro každé $n$ sestrojí v čase $p(n)$ hradlovou síť $B_n$ s $n$ vstupy a jedním výstupem, která řeší $L$.

• intuice – počítače jsou jakési složité booleovské obvody, jejichž stav se mění v čase
• uvažme nějaký problém $L\in P$ a polynomiální algoritmus, který jej řeší
  • pro vstup velikosti $n$ algoritmus doběhne v čase $T$ polynomiálním v $n$ a spotřebuje $\mathcal{O}(T)$ paměti
  • stačí nám tedy „počítač s pamětí velkou $\mathcal{O}(T)$”
    • booleovský obvod velikosti polynomu v $T$ a tedy i v $n$
  • vývoj v čase – sestrojíme $T$ kopií tohoto obvodu, každá z nich bude odpovídat jednomu kroku výpočtu a bude poropojená s minulou a budoucí kopií
• máme booleovský obvod, řešící problém $L$ pro vstupy velikosti $n$, který je polynom. velký vzhledem k $n$

Úprava definice NP: Budeme chtít, aby nápověda $y$ měla pevnou velikost závislou pouze na velikosti vstupu: $|y| = g(|x|)$ (napísto předchozího $|y| \le g(|x|)$)

• úprava je BÚNO (stačí původní nápovědu doplnit na požadovanou délku nějakými „mezerami”)

NP-úplnost obvodového SATu

• na vstupu je hradlová síť s $n$ vstupy a jedním výstupem

  • můžeme přivést na vstupy takové hodnoty, aby byl výsledek True?

• obecnější než běžný SAT

• je v $\text{NP}$ – stačí si nechat poradit vstup, udělat toposort sítě a spočítat hodnoty hradel

• je v $\text{NP}$–hard

  • mějme $L \in \text{NP}$, o němž chceme dokázat, že se dá převést na obvodový SAT
  • když nám někdo předloží vstup $x$ délky $n$ spočítáme velikost nápovědy $g(n)$
  • algoritmus $K$ kontrolující správnost nápovědy $y$ je v $\text{P}$
  • dle lemmatu umíme sestrojit obvod, který pro konkrétní velikost vstupu $n$ počítá to, co $K$
    • vstupem je $x$ a nápověda $y$
    • výstup je, zda je nápověda správná
    • velikost obvodu je také polynomiální – $p(n+g(n))$
  • v obvodu zafixujeme vstup $x$, čímž máme obvod se vstupem jen $y$
    • můžeme za $y$ dosadit nějaké hodnoty, aby na výsledku bylo True?
      • doslova otázka jak při převádění
  • pro libovolný problém z $\text{NP}$ dokážeme sestrojit funkci, která pro každý vstup $x$ v polynomiálním čase vytvoří obvod splnitelný právě tehdy, když odpověď tohoto problému na vstup $x$ má být kladná
    • to je doslova převod z daného problému na obvodový SAT $\square$

Obvodový SAT $\rightarrow$ 3,SAT

• budeme postupně budovat formuli v CNF
• každý booleovský obvod se dá v polynom. čase převést na ekvivalentní obvod pouze za pomoci hradel AND a NOT
  • stačí najít klauzule odpovídající těmto hradlům
• pro každé hradlo v obvodu zavedeme novou proměnnou popisující jeho výstup
  • v polynomiálním čase jsme schopni vytvořit formuli, která je splnitelná právě tehdy, když je splnitelný zadaný obvod

NOT

• na vstupu máme proměnnou $x$ a na výstupu $y$
• přidáme klauzule, které nám zaručí, že jedna proměnná bude negací té druhé

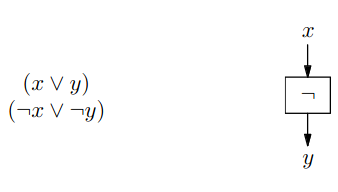
AND

• na vstupu máme proměnné $x$ a $y$, na výstupu $z$
• potřebujeme přidat klauzule, které nám popisují, jak se toto hradlo má chovat
  • lze je převést do CNF

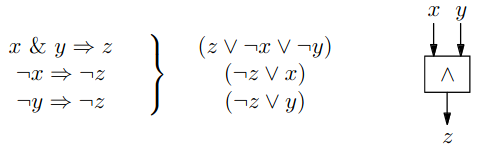
Co s NP-úplným problémem?

1. malé vstupy
   • stačí problém umlátit vhodně ořezaným exponenciálním algoritmem
2. speciální vstupy
   • na stromech – většinou lineární
   • na bipartitních grafech – většinou bude existovat polynomiální algoritmus (často odvozený od toků v sítích)
3. aproximační algoritmy – existuje docela dobrá aproximace v polynomiálním čase
   • umíme vždy dobře říct, jak daleko je aproximace od optima
4. heuristické přístupy – v některých případech bude výsledek fajn, jindy fakt mizerný
   • neumíme říct, jak daleko je výsledek od optima
5. kombinace
   • heuristické řešení může rozdělit problém na malé podproblémy, které řeší optimálně v exponenciálním čase
   • aproximační algoritmus si může zkusit pomoct heuristikou pro nalezení potenciálně lepšího řešení

Největší nezávislá množina ve stromu

Lemma: Je-li $T$ strom (funguje i pro lesy :evergreen_tree::deciduous_tree:) a $l$ jeho list, pak alespoň 1 největší nezávislá množina obsahuje $l$

• nechť $M$ je nějaká největší nezávislá množina a $l$ je list
  • buďto $l \in M$ a máme hotovo
  • jinak $l$ musí mít nějakého souseda $s$, který musí být v $M$ (jinak bychom mohli přidat $l$ a $M$ by nebyla největší)
    • $(M \setminus \{s\}) \cup \{l\}$ je také největší nezávislá množina $\square$
• tímto způsobem můžeme pokračovat pro všechny listy

Algoritmus

• do nezávislé množiny budeme přidávat při zpětném průchodu DFS v zakořeněném stromu

Barvení intervalového grafu

• máme rozvrh hodin přednášek
• rozdělujeme přednášky mezi posluchárny tak, abychom použili co nejmenší počet poslucháren

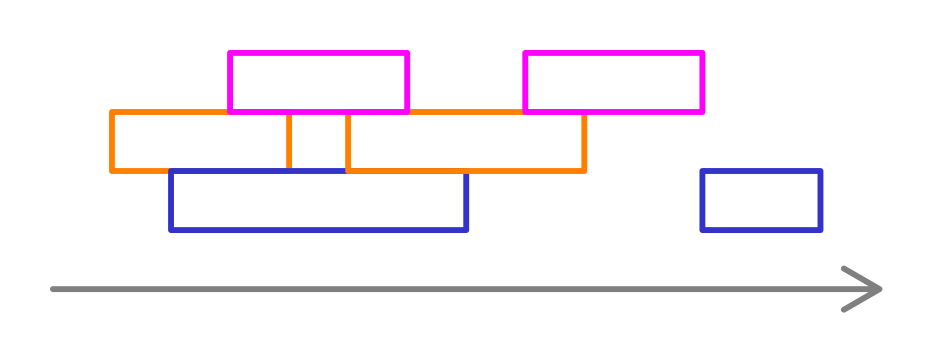
Intervalový graf:

• $V := \text{intervaly}$
• $\{u,v\} \in E \equiv u \cup v \neq \emptyset$

Algoritmus

• budeme zametat časovou přímku bodem a všímat si událostí – začátky a konce přednášek
  • kdykoliv interval začne, přidělíme mu barvu, kdykoliv skončí, barvu uvolníme
  • dalším intervalům budeme přednostně přidělovat volné barvy před přidělováním nových barev

• algoritmus opravdu použije nejmenší počet barev
  • v momentě, kdy bychom potřebovali přidat další barvičku, jsme někdy v minulosti vytvořili $b$ barev, které nyní využíváme, což znamená, že před aktuálním momentem se protínalo $b$ intervalů. Přidáním dalšího intervalu pak protínáme $b+1$ intervalů, takže potřebujeme $b+1$ barviček

Problém batohu s malými čísly

• Předměty $1,\dots, n$

• Hmotnosti $h_1,\dots,h_n$

• Ceny $c_1,\dots,c_n$

• Nosnost batohu $H$

• Hledáme podmnožinu $P$ předmětů, která se vejde do batohu a její cena je největší možná

• problém batohu je řešitelný polynomiálně tehdy, když ceny všech předmětů jsou malá celá čísla

  • chceme polynomiální algoritmus závislý na $n$ a $C=\sum_{i}c_i$

Definice: $A_k(c) := $ minimum z hmotností těch podmnožin velikosti $k$, které jejichž cena je právě $c$

• pokud žádná taková podmnožina neexistuje, $A_k(c) = \infin$

• dynamické programování

  • optimální řešení pro $k$ předmětů získáme přidáním vhodného předmětu pro optimální řešení pro $k-1$ předmětů
    • matematicky zapsáno: $A_k(c) = \min (\space A_{k-1}(c), \quad A_{k-1}(c-c_k) + h_k) \space$
  • přechod od $A_{k-1}$ k $A_k$ trvá $\mathcal{O}(C)$ – celou tabulku vyplníme v čase $\mathcal{O}(n\cdot C)$
    • maximální cena množiny, která se vejde do batohu, je největší $c^*$, pro které je $A_n(c^*) \le H$
    • nalezení tohoto $A_n$ nás stojí čas $\mathcal{O}(C)$

• ještě potřebujeme znát prvky v batohu

  • stačí si udržovat spojový seznam přidaných předmětů

• problém řešíme v čase $\mathcal{O}(n\cdot C)$

  • pseudopolynomiální – je polynomem vůči $n$ a $C$, ale není polynomem vůči velikosti vstupu ($C$ může být v binárce až exponenciálně velké, proto funguje jen s malými čísly)

Aproximační algoritmy

• máme nějakou množinu přípustných řešení a každé z nich ohodnoceno cenou $c(x)$

• mezi nimi hledáme optimální řešení s minimální cenou $c^*$

• vystačíme si s $\alpha$-aproximací – přípustné řešení má cenu $c' \le \alpha c^*$ pro $\alpha > 1$

  • relativní chyba nepřekročí $(c' - c^*)/c^*$

• poměrová chyba – poměr mezi výstupem a optimem je nejvýše $\alpha$

• relativní chyba – rozdíl mezi výstupem a optimem je … idk?

TSP – Problém obchodního cestujícího

• neorientovaný graf $G$

  • hrany ohodnoceny délkami $d(e) \ge 0$

• chceme najít nejkratší hamiltonovskou kružnici

• nechť $G$ je úplný a platí trojúhelníková nerovnost

  • $\forall x,y,z \in V : d(x,y) + d(y,z) \ge d(x,z)$

2-aproximace

• mějme minimální kostru $T$ grafu $G$

• projdeme kostru – $2T$ hran

  • tím jsme nedostali kružnici, nýbrž sled
    • upravíme – kdykoliv se při průchodu dostaneme do již navštíveného vrcholu, „přeskočíme” jej a přesuneme se až do nejbližšího dalšího nenavštíveného vrcholu
    • díky trojúhelníkové nerovnosti existují zkratky mezi vrcholy, které nám umožní kostru „obejít” $\le 2T$

Pozorování: $T \le \text{OPT}$ – když z nejkratší hamiltonovské kružnice smažeme hranu, získáme minimální kostru

• výstup $\le 2T \le 2\text{OPT}$

Nutnost trojúhelníkové nerovnosti

Věta: TSP nejde bez trojúhelníkové nerovnosti aproximovat (jinak by platilo $\text{P}=\text{NP}$)

• mějme graf $G$, doplňme jej na úplný graf $G'$

  • pokud je v $G$ hrana, tatáž hrana bude v grafu $G'$, ale s délkou 1
  • pokud v $G$ daná hrana není, bude v $G'$ s délkou $c$

• původní HK: délka $n$

• nové HK: délka $\ge n-1+c$

• pokud nastavíme $c$ dostatečně vysoké, mezera mezi $n$ a $n-1+c$ bude i přes $t$-aproximaci znatelná

  • $t\cdot n < n-1+c \implies c > (t-1)\cdot n + 1$

• dokážeme v polynomiálním čase rozhodnout, jestli v $G$ je HK $\implies \text{P} = \text{NP}$ $\square$

Problém batohu s velkými čísly

• kapacita batohu $H$

• předměty $1,\dots,n$:

  • hmotnosti $h_1,\dots,h_n$
  • ceny $c_1,\dots,c_n$

• chceme $P \subseteq \{1,\dots,n\}$ t.ž. $h(P) \le H$ a $c(P)$ je maximální

• kdybychom měli zadání ve vysokých číslech, která jsou všechna dělitelná nějakým číslem, můžeme si je přeškálovat a řešit polynomiálním algoritmem v nízkých číslech

  • když nejsou čísla škálovatelná, jejich vydělením můžeme způsobit nepřesnost

• rozsah cen při škálování $\{0,\dots,c_{max}\} \rightarrow \{0,\dots,M\}$ pro $M < c_{max}$ (nakvantované značíme $\hat{c}$)

  • každou cenu vynásobíme poměrem $M/c_{max}$ a zaokrouhlíme
    • to je to samé, jako kdybychom jednotlivé ceny zaokrouhlili na násobky čísla $c_{max}/M$
    • každé $c_i$ jsme tím změnili nejvýše o $c_{max}/M$
  • po zahození předmětů s $h_p > H$, má optimální řešení původní úlohy cenu $c(P)\ge c_{max}$
    • chyba aproximace nepřesáhne $n \cdot c(P)/M$ (kde $n$ je počet vybraných předmětů)
    • má-li chyba být shora omezena $\epsilon \cdot c(P)$, musíme zvolit $M \ge n/ \epsilon$

• když budeme hmotnosti zaokrouhlovat dolů, celé se to rozbije – mohli bychom generovat nepřípustná řešení původní úlohy (předměty se do batohu nevejdou)
• ceny zaokrouhlovat dolů můžeme $\rightarrow \hat{c}_i = \left\lfloor c_i \cdot \frac{M}{c_{max}} \right\rfloor$

Analýza složitosti

• kroky 1–3 a 5 zvládneme v $\mathcal{O}(n)$
• krok 4 řeší problém batohu se součtem cen $\hat{C} \le nM \in \mathcal{O}(n^2/\epsilon)$, což stihne v čase $\mathcal{O}(n\hat{C}) \in \mathcal{O}(n^3/\epsilon)$

Analýza chyby

• $P$ – optimální řešení původní úlohy

• $Q$ – optimální řešení přeškálované úlohy

• chceme $c(Q) \ge (1-\epsilon)\cdot c(P)$ – tedy chceme $(1-\epsilon)$-aproximaci

• jakou cenu má optimální řešení $P$ původní úlohy v nakvantovaných cenách?

• optimální řešení v nakvantovaných cenách má cenu alespoň jako řešení v původních cenách krát poměr kterým škálujeme mínus počet prvků, se kterými pracujeme

  • zaokrouhlování u jednoho prvku způsobí chybu nejvýše 1, čili dohromady nejvýše $n$

• jakou cenu má optimální řešení $Q$ přeškálované úlohy v původních cenách?

• první nerovnost platí proto, že ceny zaokrouhlujeme dolů – původní ceny jsou větší nebo rovny přeškálovaným cenám

• poslední nerovnost platí proto, že $\hat{c}(Q)$ je optimální řešení kvantované úlohy, zatímco $\hat{c}(P)$ je nějaké další řešení téže úlohy, které nemůže být lepší

• když složíme obě nerovnosti dohromady a dosadíme na $M$:

• první nerovnost platí díky dosazení za $M$

  • zlomek se odečítá a potenciálně zmenšuje, čili nerovnost je ve správném směru

• druhá nerovnost platí proto, že $c(P) \ge c_{max}$

  • já $c_{max}$ odčítám, takže ta nerovnost je ve správném směru

• Existuje algoritmus, který pro každé $\epsilon > 0$ nalezne $(1-\epsilon)$-aproximaci problému batohu s $n$ předměty v čase $\mathcal{O}(n^3/\epsilon)$ $\square$

Aproximační schéma

• aproximujeme úlohu se zadaným $\epsilon$, které nám říká omezení na chybu

• PTAS – Polynomial-Time Approximation Scheme

  • algoritmy, které pro každé $\epsilon > 0$ najdou v polynom. čase $(1-\epsilon)$-aproximaci optimálního řešení
    • aproximace s chybou $\le \epsilon$

• FPTAS – Fully Polynomial-Time Approximation Scheme

  • máme zaručeno, že je to polynomiální i s $\frac{1}{\epsilon}$
    • čas $\mathcal{O}(\text{poly}(n,\frac{1}{\epsilon}))$