Úvod do kryptografie
Toto jsou moje poznámky z předmětu “Úvod do kryptografie,” který přednášel Mgr. Martin Mareš, Ph.D. Výuka probíhala v angličtině, je tedy dost možné, že jsou některé termíny v mých poznámkách přeloženy nepřesně.
Více informací o předmětu naleznete zde.
Kryptografické útoky
Druhy útoků
- known ciphertext
- známe jen zašifrovaný text
- chceme zjistit plaintext
- known plaintext
- známe nějaký plaintext a jeho zašifrovanou verzi
- chceme zjistit klíč
- chosen plaintext
- oproti known plaintextu si jej můžeme zvolit
- chceme zjistit klíč
- rozlišovací útoky
- chceme zjistit, jestli zašifrovaný text koresponduje s určitým typem plaintextu
- např. když šifra leakuje délku plaintextu
Jak měřit obtížnost útoku
- Security level (v bitech)
- na prolomení šifry potřebujeme $2^{\text{sec. level}}$ pokusů
- pozorování: $\text{sec. level} \le \text{velikost klíče}$
„Narozeninové” útoky
- některé protokoly nebo šifry jdou docela dobře umlátit překvapivou pravděpodobností
Challenge–response autentikace
- $n$ různých noncí (nonce = number only once)
- kolik pokusů v průměru potřebujeme, než se nonce zopakuje?
- pravděpodobnost, že náhodná funkce $f$ z $[m]$ (pokusy) do $[n]$ (nonce) je prostá
- $P = \frac{\text{\#prostých f}}{\text{\#všech f}} = \frac{\frac{n!}{m!}}{n^m} = 1 \cdot (1-\frac{1}{n}) \cdot (1-\frac{2}{n}) \cdot \dots \cdot (1-\frac{m-1}{n})$
- aproximujeme $1-\frac{1}{n} \approx e^{-\frac{1}{n}}$ a tedy $P \approx e^{-\frac{1+2+\dots + m-1}{n}} = e^{-\frac{m(m-1)}{2n}}$
- pro $P[\text{kolize}] = \frac{1}{2}$
- to znamená, že $m \approx n^{\frac 1 2}$
- security level funkce s $P[kolize] = \frac 1 2$ je poloviční než velikost klíče
Welcome message
protokol:
Alice vygeneruje náhodný klíč $k$ a pošel jej po side-channelu Bobovi
Alice pošle welcome message (známý plaintext) šifrované klíčem $k$
Pak posílá další zprávy šifrované klíčem $k$
útočník si může předpočítat uvítací zprávy pro $a$ náhodných klíčů (množina $A$)
- pak poslouchá $m$ relací a čeká, až se objeví některý z předpočítaných klíčů

pro $m \cdot a \approx n$ je to jen nějaká docela reasonable konstanta
trade-off mezi časem na předvýpočet a délkou samotného útoku
Jednorázové klíče
Vernamova šifra a.k.a. One-time Pad
zpráva $x \in \{0,1\}^n$
perfektně náhodný klíč $k \in \{0,1\}^n$
zašifrovanou zprávu získáme pomocí funkce $\text{xor}$ (tím i dešifrujeme, protože $\text{xor}$ je sám sobě inverzní)
- $E$ – šifrovací fce, $D$ – dešifrovací fce
pozor! zprávu nikdy nesmíme zopakovat klíč
- útočník může zprávu triviálně měnit
- pro dvě zprávy $x, x'$ a klíč $k$ – $(x \oplus k) \oplus (x' \oplus k) = x \oplus x'$
- Sověti ve WW2 whupsík dupsík
- útočník může zprávu triviálně měnit
pokud nám zašifrovaný text nedává žádnou informaci o plain textu, šifra je perfektně bezpečná
Věta: pokud má perfektně bezpečná šifra $n$-bitové zprávy a $k$-bitové klíče, pak $k \ge n$
- to znamená, že One-time Pad je to nejlepší, co můžeme mít
Důkaz:
- angličtina wat
- množiny všech plaintextů a všech zašifrovaných textů jsou velikosti $2^n$
- počet možných klíčů je $2^k$ – čili počet možných zobrazení mezi těmito množinami
- pro spor předpokládejme, že $k < n$
- pak $2^k < 2^n$ a musí existovat nějaké 2 plaintexty $x$ a $x'$ a zašifrovaný text $y$, že $x$ je možné zašifrovat na $y$ pomocí nějakého klíče, ale $x'$ nikoliv
proto $P[D(y,k)=x] > 0$,
ale $P[D(y,k) = x'] = 0$
- rozdělení není rovnoměrné a šifra není perfektně bezpečná, spor
Dělení tajemství
- zpráva zašifrovaná několika klíči – musíme mít všechny klíče, abychom byli schopni zprávu dešifrovat
- $\oplus$ je komutativní, nice
$(k,l)$-prahové schéma
a.k.a. Shamir scheme
rozděluje zprávu na $k$ částí tak, že:
- libovolných $l$ částí určí celé tajemství $x$
- žádných $l-1$ částí nic neprozradí
$(k,2)$
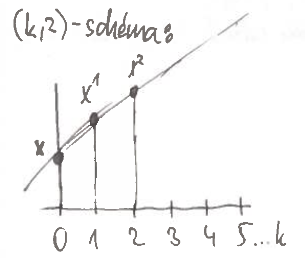
- hledám $f(t) = a\cdot t + b$ takové, že:
- $f(0) = x$ a $f(1) \in_R \Z_p$ ($\in_R$ znamená, že volba je perfektně náhodná)
- taková $f$ existuje právě 1
- pak volím $x^1 = f(1), \dots, k^k = f(k)$
- $f(0) = x$ a $f(1) \in_R \Z_p$ ($\in_R$ znamená, že volba je perfektně náhodná)
- libovolná dvě $x^i, x^j$ jednoznačně určí $f$, ale pokud známe jen $x^i$, všechna $x$ jsou stejně pravděpodobná
- každému odpovídá právě jedna $f$
Obecně
- $f:=$ polynom stupně menšího než $l$ nad konečným tělesem (uvažujeme $\Z_p$)
- $f(0)=x$
- $f(1), \dots, f(l-1)$ volím náhodně
- rozdám části $f(1)$ až $f(k)$
- pokud znám $l$ částí, určím jednoznačně $f$ (Lagrangeova interpolace)
- pokud znám $c < l$ částí:
- pokud libovolně nastavím dalších $l-c-1$ částí, každá volba $x$ určí právě jednu $f$
- všechna $x$ jsou stejně pravděpodobná (yippeee)
- pokud libovolně nastavím dalších $l-c-1$ částí, každá volba $x$ určí právě jednu $f$
Symetrické šifry
Proudové
- generují keystream, se kterými se data xorují
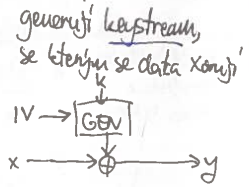
- vlastně Vernamova šifra s pseudonáhodným generátorem
- $E = D$ – funkce pro šifrování a dešifrování je ta stejná ($\oplus$ je komutativní)
- přehození bitu $x_i$ přehodí $y_i$
- NIKDY!! nechceme opakovat IV
Blokové
- šifrují bloky pevné délky $b$
- $E: \{0,1\}^b \times \{0,1\}^K \rightarrow \{0,1\}^b$
- $E_K: \{0,1\}^b \rightarrow \{0,1\}^b$
- permutace na $\{0,1\}^b$
- delší zprávy šifrujeme po blocích a případně přidáváme padding
Bezpečnost
- velmi těžké definovat formálně
- Idea: šifru nelze efektivně rozlišit od náhodné permutace
- verifikátor dostane orákulum, které vrací buďto $E_K$ pro náhodné $K$, nebo náhodnou permutaci
- úkol verifikátoru je říct, kterou variantu vrací
- může pokládat více dotazů
- chceme, aby nešla dosahnout $P[\text{úspěch}] \ge \frac{2}{3}$ s lepší složitostí než $\approx 2^{\text{security level}}$
- TLDR: dobrá bloková šifra je ta, která vypadá docela náhodně
- reálné šifry jsou prakticky vždy sudé permutace (lolol)
- verifikátor dostane orákulum, které vrací buďto $E_K$ pro náhodné $K$, nebo náhodnou permutaci
- tohle nepokrývá chosen-key/related-key útoky :(
Iterovaná šifra
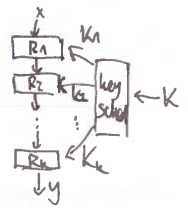
substitučně-permutační sítě
- během jednoho kola:
- vstup se vyxoruje s tajným klíčem $K_i$ (kde $i$ je číslo kola)
- whitening – omezuje kontrolu útočníka nad vstupy do S-boxů
- výstup se přesměruje do mnoha S-boxů – confusion
- malé invertibilní tabulky
- permutace na hodnotách vstupu
- výstupy s-boxů se spojí do P-boxu – diffusion
- permutace na pozicích S-boxů v bloku
- také invertibilní, stačí použít inverzní permutaci
- vstup se vyxoruje s tajným klíčem $K_i$ (kde $i$ je číslo kola)
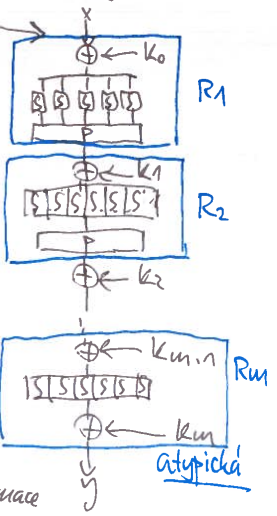
- všechny části šifry jsou invertibilní
- xor a P komutují, můžeme tak xory a P správně popřesouvat a najednou máme znova SPN
- inverze SPN je opět SPN!
Feistelovy sítě
- konstrukce s neivertibilními S-boxy
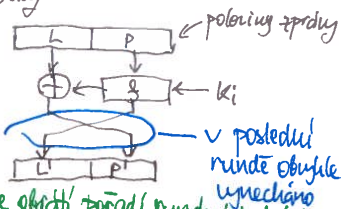
- zprávu rozdělíme na 2 poloviny
- pravou polovinu zakódujeme pomocí neinvertibilní $f$ a tajného klíče $K_i$
- Feistelova funkce – může být libovolná
- prohodíme pravou a levou polovinu a pokračujeme od bodu 2
- inverze je zase Feistelova síť, jen se obrátí pořadí klíčů $K_i$
DES (Digital Encryption Standard)
- vyvinut začátkem 70. let v IBM na zakázku NBS
- do vývoje mluvila NSA
- 56-bitový klíč (technicky 64, ale každý byte má parity bit)
- Feistelova síť s 16 iteracemi
- NSA na poslední chvíli vyměnila S-boxy (sus)
- dnes už víme, že tím actually šifru zesílila proti diferenciální kryptoanalýze (technika, která se ale objevila až daleko později, huhmm)
Struktura DESu
feistelova síť s 16 koly pracující s 32-bitovými půlbloky
plus máme na začátku a na konci P-box navíc
- úplně zbytečný, navíc znepříjemňuje SW implementaci
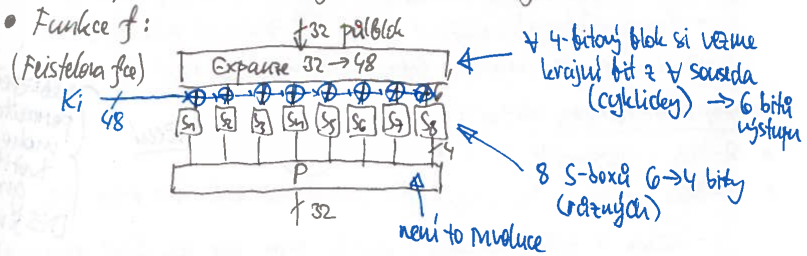
funkce $f$:
- expanduje 32 bitů na 48
- 4-bitový blok si vezme krajní bit z každého souseda (cyklicky) $\rightarrow$ 6 bitů výstupu
- 8 xorů se vstupním tajným klíčem $K_i$
- 8 lossy S-boxů – 6 bitů vstupu $\rightarrow$ 4 bity výstupu
- P-box
- expanduje 32 bitů na 48
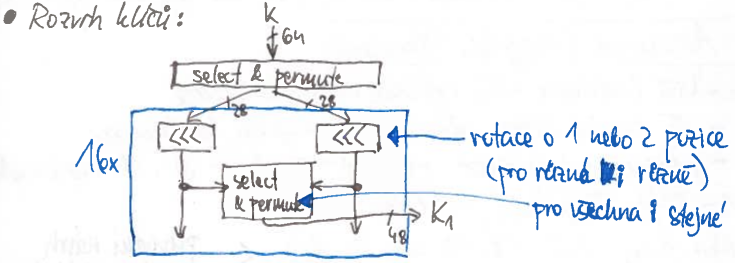
- rozvržení klíčů $K_i$ mezi iteracemi
- dostane na vstupu 56b klíč a vyprodukuje 16 klíčů o 48 b
- každý klíč obsahuje podmnožinu vstupního klíče v nějaké permutaci
- dostane na vstupu 56b klíč a vyprodukuje 16 klíčů o 48 b
Kritika DESu
- slabé klíče
- pokud $K = 0^{56}$, pak všechny $K_i = 0^{48}$
- enkrypce je identická s dekripcí – oof size max
- podobně pro samé jedničky a asi 2 další klíče
- pokud $K = 0^{56}$, pak všechny $K_i = 0^{48}$
- $E_{\bar{K}}(\bar{x}) = \overline{E_K(x)}$
- doplňky se ve Feistelově funkci (konkrétně při xorování) vyruší
- xorování s levou částí pak produkuje invers
- klíče jsou příliš krátké
- už v roce 1977 se odhadovalo, že lze postavit stroj, který vyzkouší všechny klíče za 1 den
- jen o 20 let později se to povedlo
- v roce 2012 to dokonce byla služba – mohli jste si koupi prolomení DESu na zakázku
- krátké bloky – kolize bloků jednou za $2^{32}$ bloků
Útoky na DES
- diferenciální kryptoanalýza – stačí $2^{47}$ chosen plaintextů
- lineární kryptoanalýza – dokonce jen $2^{43}$ chosen plaintextů
- to je dost na to, abychom šifru považovali za rozbitou
Pokusy o záchranu DESu
- devadesátá léta
- zkoušela se konkatenace DESu
- 2-DES – nepomůže
- sice zdvojnásobuje keysize, ale sec. level $\le 57$
- 3-DES – sec. level 113
- 2-DES – nepomůže
AES (Advanced Encryption Standard)
- 1997 – NIST (nástupce NBS) vypisuje otevřenou soutěž
- 15 návrhů šifer, několik kol veřejného hodnocení
- kritéria: bezpečnost, rychlost + snadnost na SW i HW implementaci
- vítěz: Rijandel – 2001
Struktura
- 128-bitové bloky
- variabilní délka klíče – 128, 192 nebo 256
- z toho se pak odvozuje počet kol – 10, 12 a 14
- SPN s lineární transformací
- bajtově orientovaná (pro efektivní implementaci v SW)
- každý blok má tvar matice $4 \times 4$ bajtů, klíč pro každou iteraci má stejný tvar
Iterace
ByteSub:
- bajty stavu proženeme identickými S-boxy
- S-box je inverze v galoisově tělese $GF(2^8)$ + afinní transformace z rotací a
XORů
- S-box je inverze v galoisově tělese $GF(2^8)$ + afinní transformace z rotací a
- bajty stavu proženeme identickými S-boxy
ShiftRow – $i$-tý řádek rotujeme o nějaký počet bajtů doleva
MixColumn – na každý sloupec aplikujeme stejnou invertibilní lineární transformaci
- není v poslední iteraci
AddRoundKey –
XORs klíčem- před 1. iterací dám navíc jeden AddRoundKey
- vylepšená implementace na 32-bitových procesorech
- 4 lookupy kombinující S-box s částí MixColumns
- každý sloupec je
XOR4 lookupů v tabulkách
- každý sloupec je
- na dnešních procesorech se dají některé implementace napadnout kvůli cacheování
- 4 lookupy kombinující S-box s částí MixColumns
Inverzní iterace
- některé části AES komutují
- InvMixColumn
- AddRoundKey (s nahrazeným klíčem)
- InvMixColumn komutuje s AddRoundKey, pokud $K_i$ nahradíme jeho mixem
- InvByteSub
- InvShiftRow komutuje s InvByteSub
- InvShiftRow
- jen orotovaná běžná iterace
Rozvrh klíčů
- pracuje po 32-bitových slovech
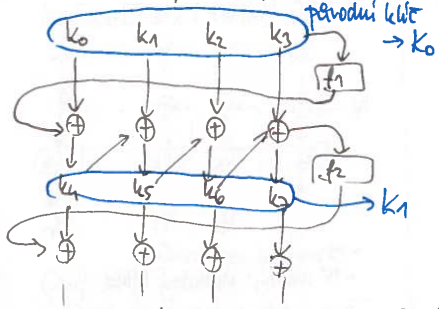
- $f_i$ je postavena z S-boxu /stejný jako šifrovací), rotace o 1 bajt a přimíchávání konstanty
Kritika AES
- jednoduchá algebraická struktura
- je možné, že se někdy najde způsob, jak tyto struktury efektivně rozbíjet řešením rovnic
- příliš malá rezerva v počtu iterací
- po nějakém čase budeme nejspíše umět rozbíjet rychleji
- jelikož je AES optimalizovaný na rychlost
- zarovnaná na byty
- difuze je až moc kontrolovaná
- i přes to se ale zatím žádný zajímavý útok neumí (krom těch implementačních, hehe)
- 128-bitový klíč není bezpečný proti kvantovým počítačům (Groverův algoritmus)
- haha, pokud věříme, že se to
- 128-bitové bloky jsou moc malé
- kolizní útoky po $2^{64}$ blocích
- stačí změnit klíč po $\approx 2^{32}$ blocích
- máme daleko méně času na to najít kolizi
- dobrá praktika in general
Použití blokových šifer
- jak šifrovat zprávy, jejíchž délka není dělitelná velikostí bloku
Padding
musí být reversibilní – nevíme totiž, jaká byla předchozí délka zprávy
varianty:
první byte paddingu je nějaká konstanta, pak doplníme samé nuly
celý padding je konstanta P = délka paddingu
celý padding jsou nuly až na poslední byte, který je P = délka paddingu
jak ale poznáme, jestli jsme přijali nepoškozenou zprávu? (chceme kontrolovat formát paddingu)
Módy blokových šifer
ECB
- Electronic Code Block
- každý blok zakódujeme stejnou funkcí a výsledky poslepujeme ve stejném pořadí dohromady
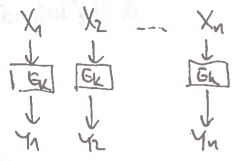
velmi jednoduché (a velmi rozbité, nepoužívat)
- leakujeme, jestli jsou nějaké bloky stejné
- nemáme žádnou náhodnou vstupní hodnotu, takže při znalosti $E_K$ jsme v loji
zajímavé vlastnosti:
- random access encryption i decription
- každý blok je nezávislý na ostatních blocích – možnost paralelizace
- bit-flip v $Y_i$ rozbije původní informace $X_i$, ale nijak neovlivní $X_j$ pro $j \ne i$
- pokud prohodíme $Y_i$ a $Y_j$, prohodíme i $X_i$ a $X_j$
- random access encryption i decription
CBC
- Cipher Block Chaining
- haha řetízkový blokotoč yeee
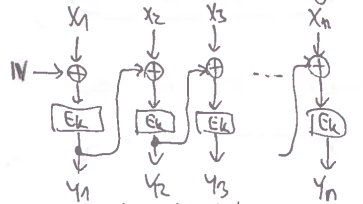
první blok vstupu vy
XORujeme s náhodným inicializačním vektoremIVa proženeme $E_K$následně každý další blok vstupu cy
XORujeme s předchozím blokem výstupu a proženeme $E_K$zajímavé vlastnosti:
- random access decription (ale né encryption)
- bit-flip v $Y_i$ změní celý $X_i$ a jeden bit v $X_{i+1}$
- vynechání/prohození dvou bloků ovlivní tyto bloky a 1 následující
Leaking
- narozeninový paradox: po $\approx 2^{b/2}$ blocích máme pravděpodobně $Y_i = Y_j$ pro $i < j$
- útočník si všiml, že se zopakovaly bloky $Y_i$ a $Y_j$
- ze
XORu předchozích bloků získá $b$ bitů informace o plaintextu
- ze
- dokud nešifrujeme moc velké zprávy, je tento leak docela vpohodě
CTR
- Counter
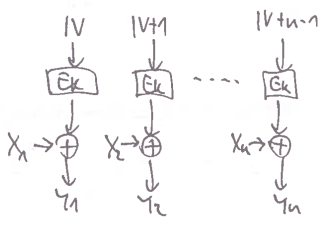
proudová šifra – padding není potřeba
nikdy nesmíme zopakovat
IV!!- bylo by to jako zopakovat one-time pad
- oproti CBC ale není potřeba, aby
IVbyl náhodný
zajímavé vlastnosti:
- bit-flip v $Y_i$ udělá akorát bit-flip v $X_i$
- random access encryption i decription
- možná paralelizace v obou směrech
Leaking
- kolik toho leakujeme, pokud jsou všechny bloky různé?
pro každou dvojici plaintextových bloků leakujeme maličkou informaci
- původní počet možností byl $2^b$, nyní je $2^b - 1$
decrease in entropy:
- pro každou dvojici bloků leakujeme $\frac 1 {2^b}$ informace
- celkový leak $\le \binom n 2 \cdot \frac 1 {2^b}$ pro $n = $ počet bloků
- leak by se rovnal tomuto číslu, kdyby byly jednotlivé leaky nezávislé
OFB
- Output FeedBack
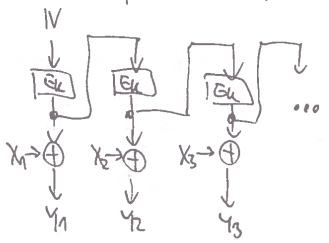
- také proudová šifra
- zajímavé vlastnosti:
- nemá žádný random access
- bit-flip v $Y_i$ udělá akorát bit-flip v $X_i$
- $E_K$ je permutace – když má moc malé cykly, stream je periodický s malou periodou a jsme v loji
Padding Oracle Attack
ukážeme pro CTR s paddingem 2. typu (celý padding je konstanta P určující velikost paddingu)
- dá se triviálně pozměnit a použít s CBC
podívejme se na poslední blok:
- předpokládejme $P \ne 1$
- budeme zkoušet všechny kombinace bit flips v posledním bajtu
- zpráva přijata $\implies$ poslední bajt změněného paddingu je
01- jelikož víme, které bit flipy vedou na
01a CTR používá jenXOR, jednoduše zjistíme původní hodnotu $P$
- jelikož víme, které bit flipy vedou na
- pak změníme všechny padding bloky na $P+1$ a flipujeme bity v posledním bytu plaintextu, než je zpráva přijata (tím získáme původní hodnotu posledního bajtu plaintextu)
- poslední bajt plaintextu přidáme k paddingu, inkrementujeme a pokračujeme pro další bajty
- pokud $P = 1$
- všechny bit-flipy v předposledním bajtu zprávy vedou na korektní padding
- předpokládejme $P \ne 1$
Další zajímavé blokové šifry z finále AES
Serpent
- 128b bloky, 128-256b klíč, 32 iterací SPN + lineární transformace
- velmi konzervativní, veeeelmi pomalé
Twofish
- 128b bloky, 256b klíč, 16 iterací feistelovské sítě
- S-boxy jsou vypočítávány z klíče
- pomalá inicializace, měnění klíče je velmi časové náročné
Proudové šifry
- historicky populární – je jednoduché je implementovat na hardwaru
- známe jich ale docela málo
- nejde na ně použít Padding Oracle Attack
LFSR
- Linear-Feedback Shift Registers
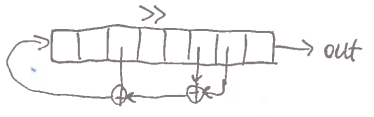
- bitshiftujeme, než vyjedeme z registru ven do outputu
- po každém shiftu vy
XORujeme všechny bity a výsledek přidáme na konec registru - problém: prvních $n$ bitů, které vyjdou z registru, je iniciální stav registru
- z dalších $n$ bitů sestavíme lineární rovnice pro klíč
- pro maximální periodu je soustava vždy regulární :skull:
- z dalších $n$ bitů sestavíme lineární rovnice pro klíč
eSTREAM project
evropský projekt hledající nové proudové šifry
2004–2008
Profile 2 (HW) – 3 šifry
- požadován security level $\ge 80$
- Trivium
Profile 1 (SW) – 4 šifry
- security level ještě větší než pro HW
- Salsa20
- z té se pak vyvinula ChaCha20 (dnes nejpoužívanější proudová šifra)
RC4
stav je klíčem vygenerovaná permutace pole $S: [0, 1, \dots ,255]$
- indexy $i$ a $j$
krok:
- $i \gets (i+1) \mod{256}$
- $j \gets (j + S[i]) \mod{256}$
- $S[i] \leftrightarrow S[j]$ – prohodím prvky na pozicích $i$ a $j$
- output: $S[(S[i] + S[j]) \mod{256}]$
init:
- 256 kroků
- k $j$ navíc přičítám $i$-tý znak klíče (opět modulo 256)
ChaCha20
následovník Salsa20
20 rund (odtud ChaCha20)
256b klíč, 64b počítadlo bloku, 64b nonce (různé verze mohou mít různá rozdělení bitů)
stav je zakódován do matice $4 \times 4$ pomocí 32bitových čísel
init:

řádek – human-readable konstanty
a 3. řádek – klíč
řádek – počítadlo a nonce
runda:
- ARX šifra – runda je kombinace sčítání, XORů a rotací
- velmi dobře implementovatelné softwarově
- ARX šifra – runda je kombinace sčítání, XORů a rotací
výsledek po 20 rundách je vy
XORován s počátečním stavem- každá runda je invertibilní funkce, bez vy
XORování je velmi jednoduché získat klíč
- každá runda je invertibilní funkce, bez vy
Hashovací funkce
$h: \times \{0,1\}^* \rightarrow \{0,1\}^b$
- v ideálním světě dokonale náhodná, jelikož je ale funkce deterministická, toto vůbec dělat nejde
požadavky na hashovací fci:
- nelze efektivně hledat kolize
- nelze efektivně hledat $x$ a $x'$ taková, že $h(x) = h(x')$
- nelze k danému obrazu najít nějaký jiný vzor
- pokud víme, že $h(x) = y$, pak neumíme najít $x' \ne x$ takové, že $h(x') = y$
- nelze funkci jednoduše invertovat
- pro nějaké $y$ nelze najít $x$ takové, že $h(x) = y$
- nelze efektivně hledat kolize
pozorování:
- $1) \implies 2) \implies 3)$
Merkle–Damgårdova konstrukce
kompresní funkce $f: \{0,1\}^b \times \{0,1\}^b \rightarrow \{0,1\}^b$
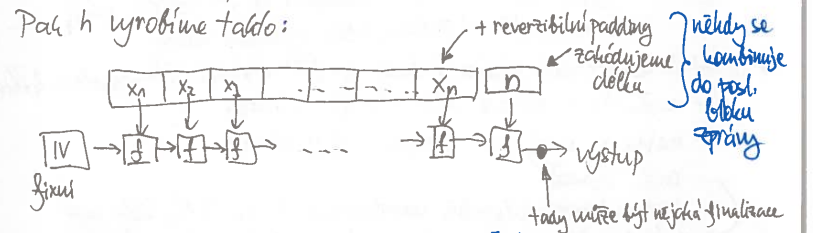
- udržujeme si nějaký stav, který pokaždé proženeme kompresní funkci dohromady s blokem kódovaného textu
konstrukce se může lišit mezi implementacemi
téměř nikdy se délka nepřidává jako samostatný blok, spíše se přidává do paddingu
vnitřní stav může být větší než blok $x_i$ – konstrukce je pak asymetrická
Věta: pokud je $f$ bezkolizní, $h$ je bezkolizní
předpokládejme, že jsme našli kolizi dvou různých vstupů v $h$, pak máme 2 případy:
- kolizní vstupy mají stejný počet bloků
- v posledním kroku jsme ke dvoum stavům přihešovávali stejnou délku $n$
- buďto byly stavy různé a našli jsme kolizi, nebo byly stavy stejné
- pokud byly stavy stejné, ale bloky různé, našli jsme kolizi, v opačném případě musel být předchozí stav stejný
- atd. atd… až na začátek, kde jsme buďto našli kolizi, nebo byly vstupy stejné, což je ale ve sporu s předpokladem, že jsou vstupy různé
- kolizní vstupy nemají stejný počet bloků
- v posledním kroku jsme k různým stavům přihešovávali různou délku $n$
- tím jsme nutně museli najít kolizi v kompresní funkci
- kolizní vstupy mají stejný počet bloků
pokud bychom na konci nepřihešovávali $n$, důkaz by nefungoval
Length extension attack
- někdo nám dal hash zprávy, ale né samotnou zprávu $z$
- z totoho hashe můžeme vyrobit validní hash odlišné zprávy $z'$, která je extension původní zprávy $z$
- pokud bychom na konci nepřihešovávali $n$, stačilo by na konec $z$ přidat námi zvolené bloky a zahešovat je s původní $z$
- pokud uživatel kontroluje hash dostatečně stupidně, dá se udělat length-extension i s přihashovaným $n$
Collision attack
s řádově $2^{\frac{b}{2}}$ vstupy dokážeme s rozumnou pravděpodobností najít kolizi
- tím ale potřebujeme i $2^{\frac{b}{2}}$ paměti (a to jako seženu kde??)
lze s konstantní pamětí se stejnou časovou složitostí
zvolíme náhodnou první $b$-bitovou zprávu $x_1$, pak $x_{i} = h(x_{i-1})$
- nekonečná posloupnost $b$-bitových zpráv
budeme hledat hodnotu, která se v posloupnosti opakuje
grafový pohled: vrcholy jsou $b$-bitové zprávy, hrany představují aplikování $h$
každý vrchol má jedinou výstupní hranu
tento graf je konečný, ale my produkujeme nekonečnou posloupnost, nutně se tedy někdy musíme zacyklit – „lollypop graph”
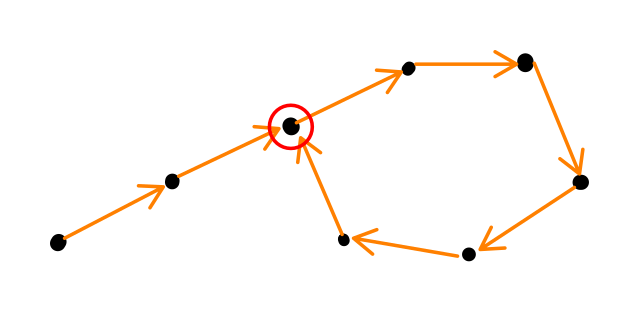
snažíme se najít spoj cyklu (červeně vyznačený vrchol) a oba jeho předchůdce (hledaná kolize)
celý graf je na paměť samozřejmě moc velký
- trik s dvěma běžci různých rychlostí:
- $T$ – v každém kroku projde 1 hranu
- $H$ – v každém kroku projde 2 hrany
- běžci se po nějaké době nutně potkají a stane se tak někde na cyklu
- nyní zastavíme $H$ a pustíme do grafu od začátku další $T'$
- tito běžci se opět po nějaké době potkají
- první fáze ($T$ + $H$) trvala $s$ kroků – $H$ je na pozici $2s$, $T$ je na pozici $s$
- v druhé fázi ($T$ + $T'$) za dalších $s$ kroků je $T$ na pozici $2s$, kdežto $T’$ na pozici $s$
- to je stejná pozice, jako ta, na které jsme skončili první fázi, čili běžci se museli potkat
- běžci se mohli potkat už dřív a první setkání nutně muselo proběhnout ve spoji cyklu
- trik s dvěma běžci různých rychlostí:
Multi-Collisions
můžeme jeden vstup zahashovat více funkcemi a výsledky konkatenovat
pokud ale alespoň jedna funkce je Merkle-Damgårdovského typu, výsledná síla není o moc větší
$x_1, x_1': f(IV, x_1) = f(IV, x_1')$ – výsledek pojmenujeme $y_1$
$x_2, x_2' : f(y_1, x_2) = f(y_1, x_2')$ – výsledek pojmenujeme $y_2$
$x_3, x_3' : \dots$
- stačí najít $k$ kolizí kompresní funkce, abychom našli $2^k$ kolidujících zpráv
- všechny možné kombinace $x_i$/$x_i'$ se totiž zobrazí na stejný hash
- na těchto zprávách pak jdou najít kolize ostatních ne M-D funkcí
tento problém je známý jen pro collision-resistance, pro invertibility-resistence je konkatenace docela fajn řešení
Parametrizované zprávy
chceme někomu dát podepsat dokument, který se jemu zdá být dobrý, ale my pak podpis přeneseme na naši zprávu, která má stejný hash
předchozím útokem najdeme pravděpodobně jen kolizní zprávu, která je nějaký hrozný garbage a nedává smysl
připravíme si pro kusy zprávy 2 sémanticky ekvivalentní ale textově odlišné varianty
- $b$ odlišných míst, nám dává $2^{b}$ možných variant zprávy
- zde už je docela slušná šance, že mezi nimi bude kolize
Innocent/Evil messages
- máme 2 množiny zpráv – innocent a evil
- chceme mezi nimi najít dvojici takovou, že se zahashují na stejný hash
- pomocí parametrizace vyrobíme $2^{\frac b 2}$ innocent a $2^{\frac b 2}$ evil zpráv
- problém: alespoň jednu z těchto množin si musíme udržovat v paměti
- můžeme vyrobit jiné množství innocent/evil zpráv a pamatovat si menší množinu za cenu horšího
- problém: alespoň jednu z těchto množin si musíme udržovat v paměti
Daviesova-Meyerova konstrukce
- konstrukce kompresní funkce z blokové šifry
- předpokládejme, že velikost bloku je stejná jako velikost klíče = $b$
- $f(a,b):= E_a(b) \oplus b$
- zašifrované $b$ s klíčem $a$
- pozor! $a$ i $b$ mohou být kontrolovány útočníkem
- zašifrované $b$ s klíčem $a$
Esencialita xorování
- pokud bychom nexorovali:
- $f(a,b) = y$, tedy $y = E_a(b)$
- najdeme kolizi $f(a',b') = y$
- $a'$ jakékoliv, $b' := D_{a'}(y)$
- $f(a', b') = f(a', D_{a'}(y)) = E_{a'}(D_{a'}(y)) = y$
- hledání kolizí je pak velmi jednoduché
Proč nepoužívat s DES
DES je komplementární
- $E_{\bar{K}}(\bar{x}) = \overline{E_K(x)}$
$f(\overline{a}, \overline{b}) = E_{\overline{a}(\overline{b})} \oplus \overline{b} = \overline{E_{a(b)}} \oplus \overline{b} = E_{a(b)} \oplus b = f(a,b)$
- hupsík dupsík
- opět triviální na hledání kolizí
Merkle Trees
- rozdělíme data do bloků a zahashujeme každý blok
- bloky konkatenujeme do větších bloků a zahashujeme
- iterujem ke kořeni
- dobrý způsob, jak na dálku verifikovat velké objemy dat
- pošleme jen list a cestu ke kořeni
- používáno interně gitem
- problémky:
- neumíme rozlišit hash podstromu od hashe kořene
- útočník může tvrdit, že nějaký vnitřní vrchol je ve skutečnosti list
- jiná sekvence, která se zahashuje do stejného kořene, whoopsie daisyyy
- řešení: požadujeme fixní hloubku stromu a u každého vrcholu si poznamenáme, jestli je to kořen nebo list
Sakura
- basically Merkelovy stromy, akorát se SHA
Používané hashovací funkce
MD5
- Rivest 1992
- Message Digest
- Merkel-Damgårdova typu
- 128b výstup
- ve dnešní době už docela malé
- od roku 2004 už umíme produkovat kolize dost rychle (cca za 10 sekund na běžném laptopu)
- nikdy nikdo ale nenašel způsob, jak MD5 invertovat
SHA-1
NSA 1995
- nikdo NSA moc nevěří, ale po mnoho let to bylo to nejlepší, co jsme měli
160b výstup
od roku 2017 už umíme produkovat kolize, ale je to dost drahé
Merkel-Damgårdova typu s Davies-Mayerovskou kompresní funkcí
- kompresní funkce pochází z blokové šifry SHACAL
SHA-2 family
- NSA
- 224b až 512b výstup
- už docela reasonable security level, ale může být docela pomalá
- aktuálně nejpopulárnější s 256 b
- podobné SHA-1, ale udržuje si daleko větší vnitřní stav a má daleko více rund
- nikdo zatím (snad) nenašel způsob, jak ji rozbít
SHA-3
- vznikla jako výstup soutěže od NIST v roce 2015
- funguje na úplně jiném principu než ostatní funkce
- „houbová funkce”
Sponge construction
2 fáze – „nasávací” a „vymačkávací”
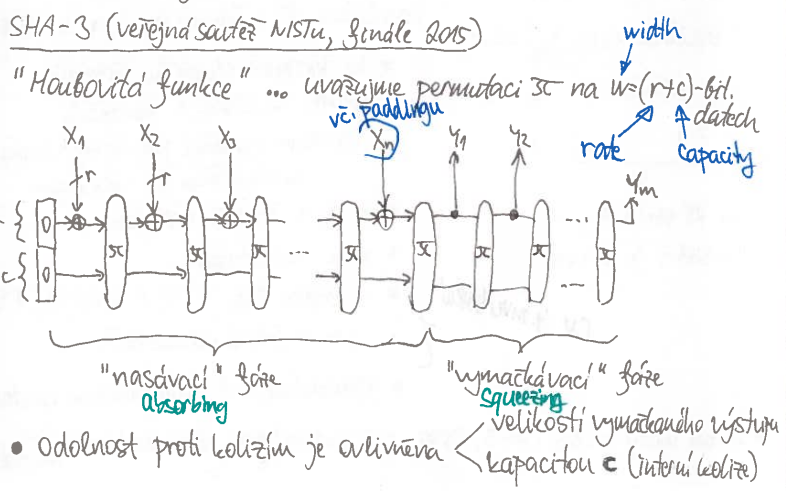
nasávací fáze
horní část stavu ($r$ bitů) se vždy xoruje s $r$ bity vstupních dat
dolní část stavu se zachovává
zamícháme horní a dolní stav permutační funkcí $\Pi$
- poslední blok má nějaký padding
vymačkávací fáze
horní část stavu odešleme jako část výstupu
dolní část stavu se zachovává
zamícháme horní a dolní stav permutační funkcí $\Pi$
permutační funkce $\Pi$ na $w = r + c$ bitech
- označme $i$-tý horní stav jako $a_i$ a dolní jako $b_i$
- $r$ – rate
- čim vyšší, tim rychlejší
- $c$ – kapacita
- pokud je moc malá, můžeme zaútočit na vnitřní stav
- jako vstup budeme používat samé nuly
- po řádově $2^{\frac c 2}$ krocích bude některý dolní stav $b_i$ stejný jako jiný $b_j$ (pro $i < j$)
- vnitřní kolizi budeme chtít zneužít pro hledání kolizních zpráv
- message A = $0^i$ ($i$ nulových bloků) – stav $(a_i, b_i)$
- message B = $0^{j-1}(a_i \oplus a_j)$ ($j-1$ nulových bloků a pak xor $a_i$ a $a_j$) – stav $(a_i, b_i)$
- security level je nejvýše $\frac c 2$
- pokud je moc malá, můžeme zaútočit na vnitřní stav
Keccak permutation
1600 bitů (damn, toje dost :eyes:)
SHA3-224
- chceme security level 224 $\implies$ použijeme $c = 448$ (a tedy $r=1152$)
- potřebujeme jen 224 bitů výsledku, stačí použít výstup z poslední rundy nasávací fáze
SHA3-512
- $c = 1024$, $r = 576$
XOF
extendable output functions
- vymačkávají output asi donekonečna
- vlastně pseudonáhodné generátory parametrizované nějakým seedem
SHAKE-128
- $c = 256$
SHAKE-256
- $c=512$
Message Authentication Codes
- zkráceně MAC
- funkce $\text{Sign}(X, K)$ a $\text{Verify}(X, K, \text{sig})$
- $X$ – message, $K$ – key, $\text{sig}$ – signature
- cílem útočníka je nechat podepsat špatnou zprávu stejným klíčem, jako by byla podepsána dobrá zpráva
Způsoby implementace
$\text{Sign}(X,K) := h(K || X)$
- hash konkatenace klíče se zprávou
- pokud je hashovací funkce založená na Merkle–Damgårdově konstrukci, lze snadno rozbít
- útočník přidá na konec plaintextu nějaký padding a extension
- pokud útočník zná stav na konci $h(K || X || \text{padding})$, pak jednoduše zjistí stav na konci $h(K || X || \text{padding} || \text{extension} || \text{padding})$
- nevim jak ale whatever
- funguje s SHA3 – standardizované pod jménem KMAC
$\text{Sign}(X,K) := h(X||K)$
- I am fucking lost
$\text{Sign}(X, K := h(h(K || X)))$
- taky prej docela bezpečný?
HMAC
- $HMAC_h(X,K) := h(K_1|| h(K_2||X))$
- kde $K_1 = K \oplus C_1$ a $K_2 = K \oplus C_2$ pro nějaké konstanty $C_1$ a $C_2$
- idea: máme nějaké dvě komponenty
- vnitřní komponenta musí být bezkolizní (nemusí být imunní vůči extension útoky)
- vnější komponenta pracuje s konstantně velkými vstupy – imunní vůči extension útoky
Kombinování šifer a MAC
Encrypt and MAC
- šifrování a vytvoření MAC probíhá nezávisle na sobě
- pošleme konkatenaci
- information leak: 2 stejné zprávy budou mít stejný MAC
MAC then encrypt
- podepíšeme plaintext a zašifrujeme konkatenaci plaintextu s podpisem
- je daleko těžší ovlivnit input šifrovací funkce
- skoro všechny implementace vedou na útoky padding orákulem
- pokud použijeme blokovou šifru, mezi MAC a šifrovací funkcí je skrytá vrstva přidávající padding na konec podepsané zprávy
- vezmeme nějakou zprávu, rozšifrujeme ji, odstraníme nějaký padding a ověříme MAC
- čas strávený ověřováním MACu závisí na tom, kolik paddingu jsme odstranili
Encrypt then MAC
- zašifrujeme plaintext a podepíšeme výsledek
- pokud útočník jakkoliv změní zašifrovanou zprávu, je ihned zastaven MACem
Konstrukce MAC bez hashovací funkce
CBC-MAC
CBC mód blokové šifry
- první blok je vyxorován s IV
- každý další blok plaintxtu je xorován předchozím blokem zašifrovaného textu
- jako output využijeme poslední blok zašifrovaného textu
IV musí být zahardkóděný v protokolu
- útočník může změnit bit v prvním bloku plaintextu a odpovídající bit v IV a máme kolizi
pokud leakne nějaký vnitřní stav
- útočník zkrátí zprávu a bude tvrdit, že tento leaknutý vnitřní stav je podpis
- pokud leakuje vnitřních stavů více, můžeme poslepovat několik zpráv dohromady se správnými podpisy – reassemble attack
- to btw znamená, že bychom nikdy neměli poslat zprávu, která je prefixem jiné zprávy (oof)
- fix: na začátek zprávy připojíme její délku
bezpečná proti chosen-plaintext útokům za předpokladu, že bloková šifra je ideální
Shannonovsky bezpečný MAC
- předpokládáme one-time klíč
- $K \in_R \mathcal K$
- rodina 2-nezávislých hashovacích funkcí (takové ty klasické hashovací funkce z ADS1)
- zdrojová množina $X$ , cílová množina $Y$
- zprávy $\in X$ a podpisy $\in Y$
- $MAC(X,K) := h_k(x)$
pokud známe validní dvojici zprávy a podpisu nám nepomůže s paděláním podpisů jiných zpráv
z libovolné dvojice zprávy a podpisu nelze dobře zjistit, jestli je to validní pár
- z definice podmíněné pravděpodobnosti (a definice 2-nezávislého systému, viz níže):
Hashovací funkce
- $\mathcal H := \{h_K \;| \;K \in \mathcal K\}$
- $\forall K \; h_K : Y \to Y$
- $\forall x, x' \in Y \; x \ne x \; \forall y, y' \in Y: P_{h\in \mathcal H}[h(x) = y \;\and \; h(x') h(y')] = \frac 1 {|Y|^2}$
- naše definice rodiny 2-nezávislých hashovacích funkcí
- česky: pravděpodobnost, že náhodná funkce $h$ z $\mathcal H$ zobrazí nějaké zvolené $x$ na $y$ a jiné zvolené $x'$ na $y'$ je stejná jako pro perfektně náhodnout funkci
Př.: Lineární funkce
- splňují naši definici 2-nezávislých hashovacích funkcí
- $X, Y = \Z_p$
- $\mathcal K = \Z_p^2$
- takováto velikost klíčů je potřeba – klíč musí být alespoň 2krát delší než zpráva
- $h_{a,b}(x) = ax + b \mod p$
- soustava lineárních rovnic pro $a$ a $b$ má jednozančné řešení
Polynomiální MAC
- trochu horší, než Shannonovsky bezpečný MAC, ale můžeme si dovolit daleko menší velikost klíče
- pro konečné těleso $\mathbb F$
- zpráva: $X_1, \dots , X_n \in \mathbb F$
- one-time klíč: dvojice $a, b \in \mathbb F$
- $\text{Sign}(X_1, \dots, X_n\;;\; a,b) := X_1a^n + X_2a^{n-1} + \dots + X_na^1 + b$
- evaluace v lineárním čase – daleko rychlejší než Shannonovsky bezpečný MAC
- pokud ale známe validní dvojici klíče a zprávy, dává nám to informaci pro padělání podpisů (né ale nijak extra velkou)
GCM
Galois/Counter Mode
AEAD – Authenticated Encryption with Additional Data
dovoluje nám přidat k podpisu další data
nejčastěji se přidávají kontextová data protokolu
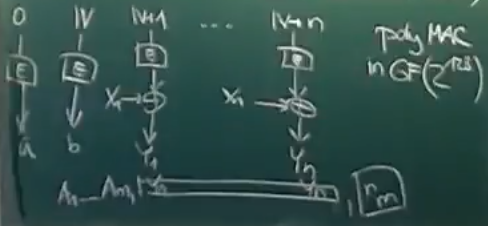
tohle v tý zkoušce prostě nebude, já to vzdávam
parametr $a$ můžeme dát fixní v poly MACu a jen generovat uniformně náhodné $b$
Poly 1305
- aktuálně populární s ChaCha20
- velmi optimalizované pro dnešní HW
Náhodné generátory
- požadavky:
- útočník ani se znalostí předchozího výstupu neumí efektivně předpovídat budoucí výstup
- statistická rovnoměrnost
- (útočník by také neměl umět výstup ovlivnit)
- útočník ani se znalostí předchozího výstupu neumí efektivně předpovídat budoucí výstup
Možná řešení
- PRNG – pseudo-random number generator
- např. AES v CTR módu
- statisticky ok, pokud není vstupní posloupnost moc dlouhá
- stačí po nějaké době vygenerovat klíč pro AES znova
- např. AES v CTR módu
- physical randomness
- rádiový šum
- útočník může přijít a poslouchat ten samý noise, co já používám pro generování
- šum na rezistoru/diodě – termální
- útočník může generátor výrazně zchladit nebo zahřát a nechat tak ADCčko generovat dlouhé monotónní stringy
- actually se to děje docela často (imagine polít platební kartu tekutým dusíkem)
- radioaktivní zářič
- měření intervalů mezi zachycenými vyzářenými $\beta$-částicemi
- uhhh, tenhle generátor asi nebude úplně nejčastější :skull:
- video $\rightarrow$ hash
- snímání lávové lampy (cloudflare moment)
- když vypnu světlo v místnosti tak dostanu samý nuly (lol)
- kruhový oscilátor
- útočník může měnit napětí na zdroji tak, aby napětí oscilovalo stejně, jako kruhový oscilátor
- timing kláves/disku/sítě
- budeme timing měřit velmi veelmi přesně a jako výstup brát nejnižší bity výsledku
- měření sítě – útočník může měřit taky
- rádiový šum
- kombinace obojího
- $1)$ a $2)$ samostatně nefungují moc spolehlivě
/dev/randoma spol.- kombinace několika fyzických zdrojů + PRNG na základě ChaCha20
RDRAND– nestabilní oscilátor procesoru- pokud by se někdo pokusil ovlivnit, procesor by to pravděpodobně poznal a na něčem kolosálně umřel
- velmi příhodné místo, kam dát do procesoru backdoor
Problémy
- jak se vzpamatovat z kompromitovaného stavu?
- entropy pooling – sbíráme entropii nějakou delší dobu a přimícháváme ji do generátoru najednou
- počet bitů by měl být roven alespoň security levelu, kterého chceme dosáhnout
- odhadování entropie – těžce těžký problém
- entropy pooling – sbíráme entropii nějakou delší dobu a přimícháváme ji do generátoru najednou
- jak iniciovat po bootu?
- čekání na sesbírání dostatku entropie – uhh, to bude trvat moc dlouho
- ukládání mezi booty – rollback do předchozího stavu znamená použití stejného poolu vícekrát (au)
- zálohy, snapshoty, nebo jen rychlé zapnutí, vypnutí a znovu zapnutí počítače
Fortuna
- Ferguson, Schneier – 2003
- několik komponent
Generátor
- AES se 128b počítadlem
- každé číslo počítadla šifrujeme tajným klíčem
- přegenerováváme po $2^{16}$ blocích, ale neresetujeme počítadlo
- neresetování počítadla nám pomáhá nezacyklit se
- přegenerováváme po $2^{16}$ blocích, ale neresetujeme počítadlo
Akumulátor
sbírá entropii z mnoha míst do 32 entropy poolů $P_0, P_1, \dots P_{31}$
- každý vzorek přidává $j$-tý vzorek do $P_j \mod{32}$
jakmile $P_0$ naakumuluje dost vzorků (ale né častěji než jednou za 100 ms), přihashuje jeho obsah ke klíči generátoru a v $i$-tém kroku ještě všechny $P_j$ pro $2^i \setminus j$
- použité pooly vyprázdním
z kompromitovaného stavu se po čase sami vzpamatujeme:

Bezpěčný kanál (symetrický)
- Alice a Bob mají unikátní tajný klíč (pro každý kanál jiný)
- zkombinujeme (v každém směru):
- symetrické šifrování (třeba AES/CTR)
- MAC (konkrétně encrypt then MAC)
- sekvenční číslo 32b
- čili po $2^{32}$ zprávách chceme měnit klíče
- KDF – Key Derivation Function
- hashovací funkce z hlavního klíče
Algoritmická teorie čísel
složitost aritmetiky
- pro $b$-bitová čísla
| Operace | Složitost |
|---|---|
| $+$ | $\mathcal{O}(b)$ |
| $\cdot$ | $\mathcal{O}(b^2)$ (lze v $\mathcal{O}(b)$, ale s obří konstantou) |
| $/$ a $\%$ | $\mathcal{O}(b^2)$ |
| $x^y \mod{n}$ | $\mathcal{O}(b^3)$ |
GCD: Euklidův algoritmus
- modulící implementace
- v každé iteraci se alespoň jedno z čísel zkrátí o 1 bit
- $\mathcal{O}(b)$ iterací $\rightarrow$ čas $\mathcal{O}(b^3)$
- chytřejší implementace se dokážou dostat na čas $\mathcal{O}(b^2)$
- značení: $x \perp y \iff \gcd{x}{y} = 1$
- $x$ a $y$ jsou nesoudělná (znak $\perp$)
Bézoutovy koeficienty
- $\forall x,y \; \exist u, v : xu + yv = \gcd{x}{y}$
- lze je získat rozšířením modulící implementace Euklidova algoritmu (extended GCD)
- návod v KSP kuchařkách
Počítání modulo $N$
- $\Z_N = \{0, 1, \dots N-1 \}$
- komutativní okruh – skoro těleso, akorát nemusíme nutně mít multiplikativní inverzi
Věta: $x \in \Z_N$ má multiplikativní inverzi $\iff$ $x \perp N$
$\Z^*_N := \left\{ x \in \Z_N \; | \; x \perp N \right\}$
- multiplikativní grupa – vybereme z okruhu jen prvky s multiplikativní inverzí
- uzavřená na násobení a každý prvek má multiplikativní inverzi
- multiplikativní grupa – vybereme z okruhu jen prvky s multiplikativní inverzí
pokud je $N$ prvočíslo, multiplikativní inverzi má vše $\implies$ $\Z_N$ je těleso
- $\Z^*_N = \Z_N \setminus \{0\}$
Důkaz:
- pro které $x \in \Z_N$ existuje $y \in Z_N$ takové, že $x \cdot y \equiv 1$ ?
- ekvivalentní s otázkou, zde rozdíl $x \cdot y$ a 1 je nějaký $t$-násobek $N$
- pokud $\gcd(x,N) = 1$, máme triviální řešení pomocí Bézoutových koeficientů
- vlastně se ptáme, jestli existuje lineární kombinace prvků $x$ a $N$ taková, že je rovna $\gcd(x, N)$
- jeden z těchto koeficientů je multiplikativní inverze
- pokud $\gcd(x,N) \ne 1$, tvrdíme, že multiplikativní inverze neexistuje
- označme $\gcd(x,N) = d$
- $x$ i $N$ jsou dělitelné $d$, tudíž $xy$ i $tN$ je dělitelné $d$ a jejich rozdíl je taktéž dělitelný $d$
- protože se rozdíl rovná 1, musela by být 1 dělitelná $d$, což je ve sporu s předpoklady
Malá Fermatova věta
- pokud $x \perp p$, pak $x^{p-1} \equiv 1 \mod{p}$
- díky tomu $x^{p-2} = x^{-1}$
Eulerova věta
- zobecnění Malé Fermatovy věty
Věta: mějme $\varphi(N) := |\Z^*_N|$, pak pokud $x \perp N$, pak $x^{\varphi(N)} \equiv 1 \mod{N}$
Důkaz:
Lagrangeova věta: Je-li $G$ konečná grupa a $H$ je podgrupa $G$, pak $|H|$ dělí $|G|$
- podgrupa je podmnožina grupy uzavřená na všechny stejné operace
- nám stačí pro komutativní grupy
mějme $x \in \Z^*_N$ a posloupnost $x^0, x^1, \dots x^k$
posloupnost se bude muset nutně začít opakovat, mějme tedy $x^k$ jako první opakující se 1
proč se první opakuje jednička:
$$ \begin{align*} x^i &= x^k \\ x^0 &= x^{k-i} \end{align*} $$pokud by se $x^k$ rovnala nějakému prvku různému od jedničky, pak by musela existovat dřívější repetice
podposloupnost $x^0, x^1, \dots, x^{k-1}$ je podgrupa $\Z^*_N$ (říkejme jí třeba $H$)
- je uzavřená na násobení
dle Lagrange $|H|$ dělí $|\Z^*_N|$
protože $|H| = k$ a $|\Z_N^*| = \varphi(N)$, pak $k$ dělí $\varphi(N)$
pokud bychom pokračovali s posloupností $x^0, x^1, \dots, x^{\varphi(N)}$, dostaneme posloupnost $x^0, x^1, \dots, x^{k-1}$ zopakovanou několikrát za sebou
Teorie čísel
$\Z_N = \{0, 1, \dots N-1 \}$
- okruh (skoro těleso, akorát nemusíme nutně mít multiplikativní inverzi)
- pokud $n$ je prvočíslo, pak máme těleso
$\Z^*_N := \left\{ x \in \Z_N \; | \; x \perp N \right\}$
- multiplikativní grupa
Čínská zbytková věta (CRT)
- mějme funkci $f : \Z_N \to \Z_{N_1} \times \Z_{N_2}$ takovou, že $f(x) = (x \mod N_1 , x \mod N_2)$
- $f$ je periodická s periodou $N_1 \cdot N_2$
- pokud definujeme $N := N_1 \cdot N_2$, pak $f(x + N) = f(x)$
- $f(x+ y) = f(x) + f(y)$
- $f(xy) = f(x)f(y)$
- $f$ je periodická s periodou $N_1 \cdot N_2$
Věta: mějme $N_1, N_2 \dots , N_k$ navzájem nesoudělné a $N = \prod_i N_i$, pak $\Z_N \equiv \Z_{N_1} \times \Z_{N_2} \times \cdot \times \Z_{N_k} $
Důkaz 1
$f$ je injektivní
- pokud $f(x) = f(y)$, pak $N_1 \; \backslash \; x-y$ a $N_2 \;\backslash\; x-y$
- musí tedy platit $N \; \backslash \; x-y \implies x = y$
$f$ je surjektivní
- $f$ je injektivní funkce mezi dvěma množinami stejné kardinality
$\implies f$ je bijektivní
Důkaz 2
chceme $x : f(x) = (a_1, a_2)$
chceme najít $u_1$ a $u_2$ takové, že $f(u_1) = (1, 0)$, $f(u_2) = (0, 1)$
proč nám $u_1$ a $u_2$ stačí?
- $f(a_1u_1 + a_2u_2) \equiv f(a_1u_1) + f(a_2u_2) \equiv (a_1, 0) + (0, a_2) \equiv (a_1, a_2)$
jak najít $u_1$
- $f(N_2) = (q, 0)$, pro $q \ne 0$
- pokud $q = 1$, $u_1 = N_2$ a můžeme skončit
- jinak si všimneme, že $q \perp N_1$, tedy musí $\exist q' : q \cdot q' \equiv 1 \mod N_1$
- $f(q' \cdot N_2) = (q \cdot q', 0) = (1, 0)$
- tedy $u_1 = q' \cdot N_2$
pro $u_2$ symetricky
Výpočet $\varphi(n)$
- $\varphi(N) := |\Z_N^*|$, kde $\Z_N^* := \{ x \in \Z_N \;|\; x \perp N \}$
- pozorování pro prvočíselné $p$:
- $\varphi(p) = p-1$
- víme z definice tělesa $\Z_p$
- $\varphi(p^k) = p^k - \frac {p^k} p = (p-1) \cdot p^{k-1}$
- ptáme se, kolik čísel od z $1, 2, \dots, p^k-1$ není soudělné s $p^k$
- to je to samé, jako se ptát na nesoudělnost s $p$
- každé $p$-té číslo je dělitelné a žádné jiné není
- ptáme se, kolik čísel od z $1, 2, \dots, p^k-1$ není soudělné s $p^k$
- pro $x \perp y$ máme $\varphi(xy) = \varphi(x) \cdot \varphi(y)$
- lze vidět z CRT
- zvolíme $f: \Z_{xy} \to \Z_x \times \Z_y$
- pro číslo $a \in \Z_{xy}$ platí, že $a \perp xy \iff a \perp x \;\and\; a \perp y$
- v obrazu máme $\varphi(x)$ řádkových indexů nesoudělných s $x$ a $\varphi(y)$ sloupcových indexů nesoudělných s $y$ (z definice)
- počet splňujících dvojic v obrazu je $\varphi(x)\cdot\varphi(y)$ a jelikož je $f$ bijekce, pak je tento počet roven počtu splňujících dvojic v předobrazu
- $\implies \varphi(n)$ umíme spočítat, pokud umíme rozdělit $n$ na prvočinitele
Faktorizace
- nikdo nezná polynomiální algoritmus
- známe sub-exponenciální algoritmy
- roste rychleji, než kterýkoliv polynom, ale pomaleji, než kterákoliv exponenciála
- např. $n^{\log\log n}$
- polynomiální algoritmy na kvantových počítačích
- nikdo nebyl schopen (zatím) nikdy implementovat
- konstanty algoritmu jsou nepříjemně vysoké
Testy prvočíselnosti
- pravděpodobnostní testy
- deterministické polynomiální algoritmy (ale exponent je asi 6 :skull:)
Fermatův test
chceme zjistit, jestli je $N$ prvočíslo
pro $x \in_R \Z_N$ spočítáme $x^{N-1} \mod N$
- pokud $x^{N-1} \ne 1 \mod N$, odpovíme „složené číslo,” jinak odpovíme „prvočíslo”
- test nemá false-negatives, ale může mít false-positives
- pokud $x^{N-1} \ne 1 \mod N$, odpovíme „složené číslo,” jinak odpovíme „prvočíslo”
případy, ve kterých odpovíme, že máme složené číslo:
Eulerův svědek: $x$ takové, že $x \not\perp N$
- Eulerových svědků je pro jedno číslo generally dost málo
Fermatův svědek: $x$ takové, že $x \perp N$ a $x^{N-1} \ne 1 \mod N$
Carmichaelova čísla
- složená, ale vždy projdou Fermatovým testem
- nemají žádné Fermatovy svědky, mají jen Eulerovy svědky
- je jich naštěstí dost málo (ale stále nekonečně mnoho)
Pravděpodobnost
pokud $N$ je složené a není Carmichaelovo číslo
$H := \{ x \in \Z_N^* | x^{N-1} \equiv 1 \mod N \}$ – množina všech nesvědků
- $H$ je podgrupa $\Z_N^*$, tedy dle Lagrangeovy věty $|H|$ dělí $|\Z_N^*|$
- dokonce je ostře menší, protože $N$ není Carmichaelovo
- $|H| \le \frac{1}{2} |\Z_N^*|$
- $H$ je podgrupa $\Z_N^*$, tedy dle Lagrangeovy věty $|H|$ dělí $|\Z_N^*|$
pravděpodobnost false-positive $\le \frac{1}2$
- stačí Fermatův test iterovat mnohokrát
Rabin-Millerův test
- odhalí i Carmichaelova čísla
vybereme náhodně $x \in_R \Z_N$
pokud $\gcd(x, N) \ne 1$, $x$ je složené – Eulerův svědek
spočítáme $x^{N-1} \mod N$
- pokud výsledek není 1, $x$ je složené – Fermatův svědek
spočítáme $x^\frac{{N-1}}{2} \mod N$
spočítáme $x^\frac{{N-1}}{4} \mod N$
spočítáme $x^{\frac {N-1} {2^k}} \mod N$
…
dokud není exponent lichý
- pokud někdy dostaneme výsledek $\ne \pm 1$, máme složené číslo – Riemannův svědek
- pokud někdy dostaneme výsledek $= -1$, našli jsme prvočíslo
- pokud je $= 1$, pokračujeme
Správnost
- algoritmus nedává false-negatives
- uvažme posloupnost $x^{\frac {N-1} {2^k}}$
- každý prvek je odmocnina předchozího prvku
- pokud je některý prvek posloupnosti $= 1$, pak následující prvek je $\sqrt{1} \mod N$
- pokud je $N$ prvočíslo, pak je $\Z_N$ těleso a máme nejvýše 2 možné hodnoty odmocniny a jsou to hodnoty $+1$ a $-1$
- pokud tedy někdy v průběhu narazíme na hodnotu různou od $\pm1$, $N$ jistě není prvočíslo
- pokud je některý prvek posloupnosti $= -1$, nemůžeme pokračovat
Věta Rabin:
- pravděpodobnost false-positive $\le \frac{1}4$
Věta Miller:
- rozšířená Riemannova hypotéza
- pro $N$ složené $\exist x$ svědek $\le \mathcal{O}(\log N)$
Generování velkých prvočísel
chceme uniformně generovat náhodné $b$-bitové prvočíslo (nepočítáme leading zeros)
náhodně tipujeme bity a testujeme
- v nejhorším případě tento přístup nikdy neterminuje
hustota prvočísel kolem $N$ je cca $\frac 1 {\ln N}$
- cca $\frac 1 {\ln N}$ čísel v našem zvoleném intervalu jsou prvočísla
- protože $N$ je exponenciální vůči $b$, pak $\frac 1 {\ln N} = \frac 1 {c \cdot b}$ pro nějakou konstantu $c$
- to nám nějak docela stačí
Diskrétní logaritmus
Věta: $\Z_p^*$ je cyklická grupa (pro prvočíselné $p$)
tedy $\exist g \text{ (generátor)} : {g^0, g^1, \dots g^{p-2}} = \Z_p^*$
isomorfismus – v jednom směru umocňování, v druhém směru diskrétní logaritmus
jak ověřit, zda je $g$ generátor?
nemůžeme projít celou grupu, ta je na to moc velká :(
pokud $g$ není generátor
- mějme $g^t = 1$ první opakování jedničky (taky se předtím nikdy nic neopakuje)
- $H := \{g^0, g^1, \dots, g^{t-1}\}$ je nějaká podgrupa $\Z_p^*$
- uzavřená na násobení $g^i \cdot g^j = g^{i+j} = g^{i+j} \mod t$
- také platí, že $H \ne \Z_p^*$ (protože $g$ není generátor)
- dle Lagrange: $|H| \;\backslash\; \varphi(p) \implies t \; \backslash \; p-1$
$$
\begin{align*}
t &= \frac {p-1} k \text{ pro } k > 1 \\
\\
g^{\frac {p-1} k} &\equiv 1 \mod p \\
\end{align*}
$$
- pokud by $g$ byl generátor, pak takové $k$ neexistuje, protože první exponent, pro který bychom dostali jedničku, by byl $p-1$
zrychlení: stačí projít všechny $k$ prvočíselné dělitele $p-1$
- pro neprvočíselné $k$ s prvočíselným dělitelem $q$ máme: $$ \begin{align*} g^{\frac{p-1}{q \cdot k'}} &\equiv 1 \mod p \\ \left(g^{\frac{p-1}{q \cdot k'}}\right)^{k'} &\equiv 1^{k'} \mod p \\ g^{\frac{p-1}{q}} &\equiv 1 \mod p \end{align*} $$
pokud $g$ je generátor, je $g^t$ taky generátor?
- to se stane jen tehdy, když $t \perp p-1$
- počet generátorů je $\varphi(p-1)$, což je docela dost, takže náhodné vybírání a testování docela funguje
Diskrétní odmocniny
Modulo prvočíslo
- mějme $a$, vyřešme $x^2 \equiv a \mod p$
- pozorování: (pro $p=5$)
- $0^2 = 0$
- $1^2 = 4^2 = 1$
- $2^2 = 3^2 = 4$
- 1, 4 mají 2 odmocniny
- 2, 3 nemají žádnou odmocninu
- 0 má právě jednu (výjimka)
- počet odmocnin je vždy $\le 2$
- $x^2 = (-x)^2 \implies$ počet odmocnin je vždy sudé číslo (až na 0)
Kvadratické zbytky
čísla s přesně dvěma odmocninama
čísla se sudým diskrétním logaritmem jsou vždy kvadratické zbytky
- $(g^{k})^2 \equiv g^{2k}$
- $g^k$ je odmocnina $g^{2k}$ a jelikož počet odmocnin je vždy sudé číslo, máme kvadratický zbytek
čísla s lichým diskrétním logaritmem nikdy nejsou kvadratické zbytky
- nezbyly nám žádné odmocniny :(
Eulerovo kritérium
- algoritmus na zjišťování, zda má číslo kvadratický zbytek
Věta: $x \ne 0$ je QR $\iff x^{\frac {p-1}2} \equiv 1$
Důkaz:
- $x = g^{2k}$
- $g^{2k \cdot \frac{p-1}2} \equiv g^{k \cdot (p-1)} \equiv (g^{p-1})^k \equiv 1^k \equiv 1$
- $x = g^{2k+1}$
- $g^{(2k + 1) \cdot \frac{p-1}2} \equiv g^{2k\cdot \frac{p-1}2 + \frac{p-1}2} \equiv 1 \cdot g^{\frac{p-1}2} \equiv 1 \cdot (-1) \equiv -1$
Důsledek:
- znaménko výsledku nám řekne, jestli je $x$ QR
Modulo složené číslo
- použijeme CRT na dělitelích $n$
- pro jednoduchost předpokládejme, že $n = p \cdot q$ pro prvočíselné $p \ne q$
- dle CRT $\Z_n = \Z_p \times \Z_q$
- odmocniny můžeme počítat modulo prvočíselnými děliteli $n$
- pro $k$ různých prvočíselných dělitelů $n$ máme $2^k$ různých odmocnin nebo žádné (bez důkazu)
- pokud umíme faktorizovat $n$, umíme spočítat odmocniny
- nikdo neví, jak tohoto docílit bez rozkladu $n$ na prvočinitele
RSA
- Rivest, Shamir, Adleman – 1978
Klíč
velká prvočísla $p$ a $q$
- ve dnešní době je potřeba alespoň 4tis.-bitová velikost prvočísel
modulus: $n = p \cdot q$
- $\varphi(n) = (p-1)(q-1)$, protože $p \perp q$
- můžeme poměrně bezpečně posílat, protože je dost těžké velká čísla faktorizovat
šifrovací exponent: $e : e \perp \varphi(n)$
dešifrovací exponent: $d : d \cdot e \equiv 1 \mod{\varphi(n)}$
šifrovací klíč: $(n,e)$
dešifrovací klíč: $(n, d)$
jeden klíč nejde zjistit z druhého (nebo alespoň ne rozumně rychle)
Šifrování
zprávy jsou $x \in \Z_n$
$E(x) = x^e \mod n$
$D(y) = y^d \mod n$
Korektnost
musí platit $x \perp n$
- pokud by $\gcd(x,n) \ne 1$, pak by z $\gcd(x,n)$ vypadlo jedno z prvočísel $p$ nebo $q$
$D(E(x)) \equiv (x^e)^d \equiv x^{ed} \equiv x^{k \cdot \varphi(n) + 1} \equiv (x^{\varphi(n)})^k \cdot x \equiv x \mod \varphi(n)$
- třetí ekvivalence: $d \cdot e \equiv 1 \mod \varphi(n)$
- pátá ekvivalence: Malá Fermatova věta
Efektivita
- polynomiální, ale pomalé
- často stavíme hybridní šifru z RSA a nějaké symetrické šifry
Zrychlovací triky
- veřejný klíč:
- volím malý $e$ (třeba 3 nebo 7)
- privátní klíč:
- pokud vytvářím klíče, mohu si zapamatovat $p$ a $q$ a dešifrovat pomocí CRT (čínské zbytkové věty)
- aritmetika $\mod n$ je stejná, jako aritmetika $\mod p$ a následně $\mod q$
- počítáme s menšími čísly → rychlejší
- pokud vytvářím klíče, mohu si zapamatovat $p$ a $q$ a dešifrovat pomocí CRT (čínské zbytkové věty)
Důležité vlastnosti
- komutativní: $D_{K_2}(D_{K_1}(E_{K_2}(E_{K_1}(x)))) = x$
- klíče musí mít stejný $n$
- pozn.: mít několik klíčů se stejným $n$ není bezpečné, a tak se komutativita spíše nevyužívá
- homomorfní: $E(x \cdot y) \equiv E(x) \cdot E(y)$
- vlastnost, která většinou spíše pomáhá útočníkům
Slepé podpisy
- Bob:
- má plaintext $x$
- vybere $r \in_R \Z^*_n$ – blinding factor
- pošle Alici $x \cdot r^d$
- pokud je $r$ i $d$ náhodné, pak je $r^d$ také náhodné
- Alice:
- umocní šifrovanou zprávu svým $e$: $(xr^d)^e = x^e \cdot r^{ed} = x^e \cdot r$ a pošle Bobovi
- nikdy tak nezjistí nic o $x$
- Bob:
- $(x^er)\cdot r^{-1} = x^e$
Útoky
Špatná volba parametrů
- pokud $x < n^{1/e}$, pak stačí spočítat odmocninu v $\Z$, což je polynomiální
- známe-li $\varphi(n)$, můžeme $n$ faktorizovat:
pokud $d < n^{1/4}$, pak lze $d$ spočítat z $e$
- malý si můžeme dovolit jen veřejný exponent
známe-li $d$ i $e$, můžeme spočítat $\varphi(n)$ a máme stejný problém jako výše
Meet in the middle attack
mějme $m^e \equiv c$
- známe $e$ a zašifrovaný text $c$, snažíme se dostat zprávu $m$
- budeme hledat malá $u$ a $v$ taková, že $u^e \equiv c \cdot v^{-e}$
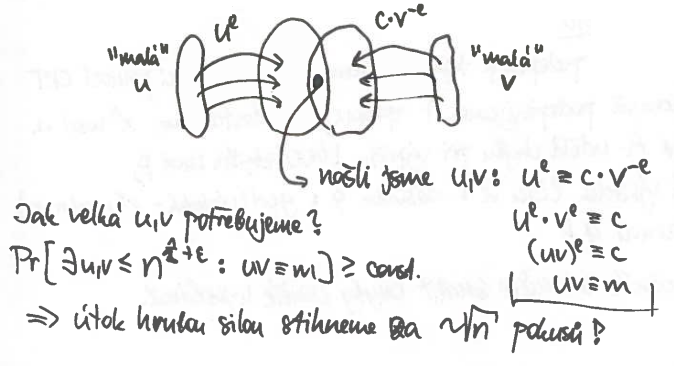
Podobné zprávy
- $x' = x + \delta$
- $c \equiv x^e$ a $c' = (x + \delta)^e$
- pokud známe $c$, $c'$ a $\delta$:
- $x$ je společný kořen polynomů $p(x) = x^e - c$ a $p(x') = (x+ \delta)^e - c'$
- to je kořen $\gcd(p(x), p'(x))$
- s velkou pravděpodobností je tento polynom lineární
- to je kořen $\gcd(p(x), p'(x))$
- $x$ je společný kořen polynomů $p(x) = x^e - c$ a $p(x') = (x+ \delta)^e - c'$
Podobná prvočísla $p$ a $q$
- $q = p + 2\delta$
- $n = pq = p(p+2\delta) = p^2 + 2p\delta$
- $n + \delta ^2 = (p + \delta)^2$
- mohu zkoušet různá $\delta$ a zkoušet umocňovat $(n + \delta)^2$, dokud to nevyjde
Několik klíčů se stejným $n$
- každý majitel privátního klíče může faktorizovat $n$
- při posílání téže zprávy více příjemcům lze jednoduše dešifrovat
Tatáž zpráva zašifrována klíči s různými $n$
- např.: klíče $(n_1, 3)$, $(n_2, 3)$, $(n_3, 3)$
- $x^3 \equiv c_1 \mod n_1$
- $x^3 \equiv c_2 \mod n_2$
- $x^3 \equiv c_3 \mod n_3$
- $N := n_1 \cdot n_2 \cdot n_3$
- pomocí CRT: $\exist y \in \Z_N \; \forall i : y\mod n_i = c_i$
- to znamená, že $y = x^3$ – hupsík dupsík
- pomocí CRT: $\exist y \in \Z_N \; \forall i : y\mod n_i = c_i$
Chyba při výpočtu
- Alice podepisuje tajným klíčem s optimalizací pomocí CRT
- opakovaně podepisuje 1 zprávu $x$, dostáváme $x^e \mod n$
- pokud Alice udělá při některém z výpočtů chybu ve výpočtu zbytku modulo $p$
- místo $x^e$ dostane $x^e + c \cdot q$
- $\gcd(c\cdot q, n) = q$ – hupsík dupsík
- pravděpodobnost, že se toto reálně stane, je velmi nízká, ale útočník může chybu uměle vyvolat (už zase poléváme platební karty tekutým dusíkem…)
- jak se bránit: výsledek si někde vedle vymodulíme 64b prvočíslem
- pokud se stala chyba v původním výpočtu, v tomto výpočtu bude pravděpodobně taky (chyba by zmizela jen tehdy, kdyby $c$ bylo dělitelné tímto prvočíslem)
- v daleko menším čísle se ověřuje správnost výpočtu jednodušeji
RSA leaks
Legenderův symbol: $\left(\frac x p \right)$ – není to zlomek, tohle je prostě notace
pro prvočíselné $p$ a $x \in \Z_p$
$\left(\frac x p \right) : = x^{\frac {p-1} 2} \mod p$
- z Eulerova kritéria:
- Legenderův symbol je zobrazení $\Z_p \to \{0, +1, -1\}$
- homomorfismus
Jacobiho symbol: $\left(\frac x n \right)$
pro liché složené $n = \prod_{i=1}^n p_i^{\alpha_i}$ a $x \in \Z_n$
$\left(\frac x n \right) := \prod_i= \left( \frac x {p_i} \right)^{\alpha_i}$
Jacobiho symbol je zobrazení $\Z_n \to \{0, +1, -1\}$
- opět homomorfní – $\left(\frac {x\cdot y} n \right) = \left(\frac x n \right) \cdot \left(\frac y n \right)$
- Jacobiho symbol je 0 tehdy, když jeden z dílčích faktorů je 0, což je tehdy, když je $x$ dělitelné jedním z faktorů $p_i$, což je tehdy, když $x \not\perp n$
Leak Jacobiho symbolu
jediný známý leak
$$ \begin{align*} \left(\frac x n \right)^e &= \left( \frac {x^e} n \right) \\ \left(\frac x n \right) &= \left(\frac {x^e} n \right) \end{align*} $$- první rovnost platí z homomorfismu
- druhá rovnost platí, jelikož je Jacobiho symbol $\pm 1$ a $e$ je liché
- plaintext a zašifrovaný text mají stejný Jacobiho symbol!
- existuje polynomiální algoritmus na počítání Jacobiho symbolu, který nepotřebuje faktorizovat (pomocí nějaký cursed Gaussovy věty)
tento leak nám dává přesně 1 bit informace
Sémantická bezpečnost RSA
- žádná vlastnost plaintextu nemá jít efektivně zjistit z cyphertextu
- $\text{parity}(y) := D(y) \mod 2$
- $\text{half}(y) := \begin{cases} 1 \iff D(y) > \frac n 2 \\ 0 \text{ jinak } \end{cases}$
Věta: pokud máme orákulum pro $\text{parity}$ nebo pro $\text{half}$, pak umíme dešifrovat v $\mathcal{O}(\text{poly}(b))$
Orákulum pro half
$y \equiv x^e \mod n$
$x = \alpha \cdot n$ pro $\alpha \in [0, 1)$
$\text{half}(y) = $ první bit $\alpha$ za desetinnou čárkou
- říká nám, jestli $x > \text{half}(n)$
$\text{half}(y \cdot 2^e) = $ druhý bit $\alpha$ za desetinnou čárkou
- homomorfismus RSA → $y \cdot 2^e = E(2x)$
můžeme iterovat
- každá iterace nás přibližuje blíže k reálné hodnotě $\alpha$
- po $\log(n) + 1$ krocích máme aproximaci $\alpha ' : |\alpha - \alpha '| < \frac 1 n$
- zaokrouhlení $n \cdot \alpha '$ nám dá $x$
Orákulum pro parity
pomocí orákula pro $\text{parity}$ umíme simulovat orákulum pro $\text{half}$:
$\text{half}(y) = \text{parity}(y \cdot 2^e)$
homomorfismus RSA → $y \cdot 2^e = E(2x)$
ve které půlce zjistíme z LSb $2x$
- samotné $2x$ je sudé, ale počítáme $\mod n$
pokud $x < \frac n 2$:
- $\text{half}(y) = 0$
- $\text{parity}(y \cdot 2^e) = 0$
pokud $x > \frac n 2$:
- $\text{half}(y) = 1$
- $\text{parity}(y \cdot 2^e) = 1$
- $2x \mod n = 2x - n$, což musí být liché číslo
Padding Schemes
- RSA je kompletně deterministické, porovnáváním šifrovaných textů tak můžeme porovnávat i plaintexty
- chceme tedy zprávy předtím nějak randomizovat
PKCS#1 v1.5
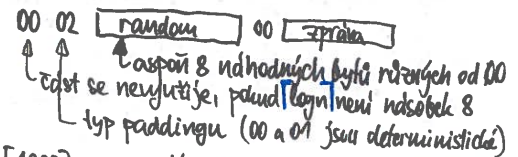
Bleichenbacherův útok
- pokud máme padding orákulum
- řekne, zda má dešifrovaná zpráva správný formát paddingu
- po několika milionech zpráv, které analyzujeme, dovedeme z v1.5 získat tajný klíč
PKCS#1 v2.0
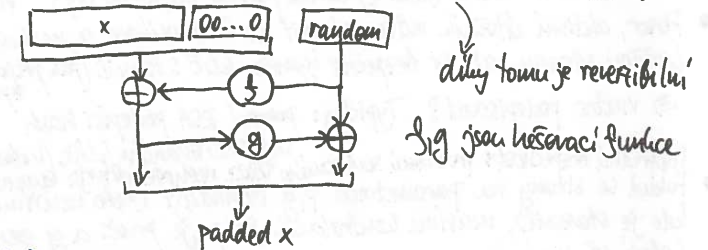
- vlastně 2-rundová Feistelova síť
- jednoduše reversovatelné
- oproti v1.5 nemá žádnou viditelnou strukturu, jako páry 00
- odolné vůči všem typům Bleichenbacherových útoků
Diffie-Hellman
protokol pro tajnou výměnu klíčů
základ ve složitosti diskrétního logaritmu
forward security
- pokud leakne privátní klíč podepisovací funkce, staré zprávy stále nejdou dešifrovat
Veřejné parametry: prvočíslo $p$ a generátor $g$ multiplikativní grupy $\Z_p^*=\{g^0, g^1, g^2,\dots\}$
Alice: vygeneruje $x \in_R \{0, \dots , p-2 \}$ a pošle Bobovi $g^x \mod p$
Bob: vygeneruje $y \in_R \{0, \dots , p-2 \}$ a pošle Alici $g^y \mod p$
- oba umí spočítat $g^{xy}$
- pokud by někdo uměl spočítat diskrétní logaritmus v rozumném čase, DH by byl rozbitý
- DH má možná jiné zranitelnosti, o kterých nikdo neví
Útoky na DH
Man-in-the-middle attack
- stačí na obě dvě strany předstírat, že jsme druhá strana
- jelikož je $g$ veřejné, stačí vygenerovat pro každou stranu jedno $x'$ a $y'$
- řešení: zprávu asymetricky podepíšeme
Útok na veřejné parametry
- některé implementace začínají dohodou na parametrech
- manipulace $g$
- útočník může za $g$ dosadit mocninu $g^k$ generující podgrupu $\Z_p^*$, která je dostatečně malá
- spočítání diskrétního logaritmu je pak snažší
- řešení: validování parametrů
Man-in-the-middle na veřejných parametrech
- pokud víme, že $g^k$ generuje podgrupu $\Z_p^*$, která je dostatečně malá
- když Alice posílá $g^x$, přepošleme Bobovi $g^{xk}$
- řešení: podepsání transkriptu protokolu
- transkript – seznam akcí, které se během protokolu staly
Information leak
- z $\left( \frac {g^x} p \right)$ lze poznat lichost $x$ (podobně i lichost $y$)
- z toho lze získat paritu $xy$ a tedy zjistit, jestli $g^{xy}$ je kvadratický zbytek (QR)
Podgrupy
$\Z_p^*$ má alespoň 2 podgrupy: $\{-1, 1 \}$ a kvadratické zbytky (QR)
mohutnost kterékoliv podgrupy dělí $p-1$ (Lagrange)
- pokud $\frac {p-1} 2$ je prvočíslo, pak už žádné jiné podgrupy neexistují
- $p = 2q + 1$
- toto $q$ je tzv. „safe prime”
místo generátoru $g$ můžeme použít $g^2$ a generovat jen QR
- tím se dokonce vyhneme information leaku
Jak se vyhnout velkým exponentům
- nechceme pracovat s moc velkými exponenty, ale zachovat protokol bezpečným
- $p = kq + 1$, kde $q$ má cca 256 b, $p$ daleko více
- pracujeme v podgrupě s generátorem $g^k$, která má $q$ prvků
- DH zůstává stále stejně těžké
Sémantická bezpečnost
- zjistit nejnižší bit je stejně těžké jako zjstit všechno – podobně jako u RSA
ElGamalův kryptosystém
použití DH pro asymetrické šifrování založené na diskrétním logaritmu
nelze použít na asymetrické podepisování – veřejný klíč lze jednoduše získat z veřejných parametrů
veřejné parametry: prvočíslo $p$ a generátor $g$ grupy $\Z_p^*$
privátní dešifrovací klíč: $k \in_R \{0 \dots p-1 \}$
veřejný šifrovací klíč: $h = g^k \mod p$
šifrování:
- $t \in_R \{ 0 \dots p-2 \}$
- $s = h^t$
- rovnoměrně náhodný prvek grupy
- $y = x \cdot s$
- posíláme dvojici $g^t$ a $y$
dešifrování:
- $s = g^{kt}$
- $x = y \cdot s^{-1}$
podobně jako RSA leakuje jestli $x$ je QR
- stačí opět vybírat zprávy jen z množiny QR
Eliptické křivky
dobrý zdroj malých grup s těžkým diskrétním logaritmem a žádnými malými podgrupami
- počítání bývá také docela rychlé
problém diskrétního logaritmu na eliptických křivkách bývá těžší, než běžně
- pokud bychom rozbili DH právě na rychlém počítání dl, eliptické křivky by to nejspíš ustály
nad reálnými čísly:
křivka = množina všech $(x,y) \in \R^2$ takových, že $y^2 = x^3 + ax + b$
- (kde $a,b$ jsou parametry takové, že $4a^3 + 27b^2 \ne 0$)
- tato podmínka zaručuje právě 3 průsečíky s osou $x$ (jinak je křivka singulární)
- (kde $a,b$ jsou parametry takové, že $4a^3 + 27b^2 \ne 0$)
např.:
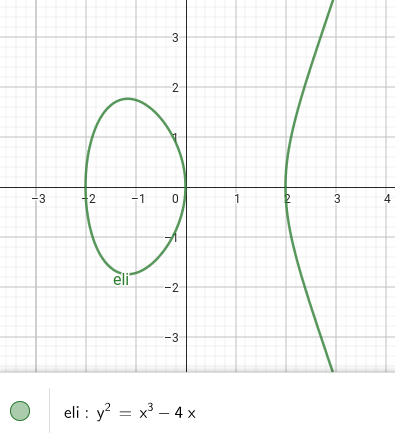
z bodů na křivce uděláme grupu s operací $+$ a neutrálním prvkem $\mathcal{O}$ – „point at infinity”
jak vypadá $P+Q$ pro $P=(x_1,y_1)$ a $Q=(x_2,y_2)$:
- $x_1 \ne x_2$:
- uvážíme přímku $PQ$, která křivku protne ve 3 bodech – $P$, $Q$ a $R$
- za výsledek prohlásíme zrcadlový obraz bodu $R$ podle osy $x$
- vlastně to znamená, že kdykoliv jsou 3 body $P$, $Q$ a $R$ na společné přímce, pak $P+Q+R = \mathcal O$
- $x_1 = x_2$ a $y_1 = - y_2$: výsledek je $\mathcal{O}$
- $x_1 = x_2$ a $y_1 = y_2$:
- vezmeme tečnu v bodě $P = Q$
- eli. křivka má jen jeden další průsečík $R$, odsud postupujeme stejně jako v 1. bodě
- $x_1 \ne x_2$:
toto je abelovská grupa
totéž lze dělat nad konečným tělesem $\mod p > 3$
- opět vzniká abelovská grupa
také funguje nad jakýmkoliv konečným tělesem $\mathbb{F}_m$
- buďto pro $m = p > 3$ nebo pro $m = p^k$, kde $p>3$
Asymetrické podpisy
- privátní podepisovací klíč a veřejný ověřovací klíč
- podepisovací a oveřovací funkce
- ověřovací funkce dostane na vstupu plaintext $x$ a podpis $\text{sign}$ a musí říct, jestli tento podpis patří k původnímu plaintextu $x$
- podepisovací funkce bývá randomizovaná, oveřovací funkce musí být tedy docela komplexní
Útoky
cíle útočníka:
- zjištění tajného klíče
- existenční padělání – schopnost podepsat zprávu, kterou jsme nikdy neviděli
- cílené padělání – schopnost podepsat předem určenou zprávu
k dispozici máme/můžeme mít:
- veřejný klíč
- known plaintext – útočník zachycuje zprávy s podpisy
- chosen plaintext – útočník nechává podepisovat vybrané texty
- většinou se snaží dostat podpis k jiné zprávě, než předložil k podepsání
RSA podpis
- tajný encryption key, veřejný decription key, $\text{sign} = x^e \mod n$
Existenční padělání
jen na základě veřejného klíče
vyberu si úplně náhodný podpis $\text{sign}$ a pošlu $x = \text{sign}^d \mod n$
pravděpodobně nesmyslná zpráva
Cílené padělání
- chosen plaintext
- můžeme použít slepé podepisování
- řešení: nebudeme podepisovat samotnou zprávu, ale hash zprávy
- tím se zbavujeme homomorfismu RSA
ElGamalův podpis
- velmi různý od ElGamal šifry
- funkce nebude vyžadována na zkoušce (thank fucking god)
DSA
digital signature algorithm
ECDSA – DSA s eliptickými křivkami
NIKDY!!!! nepoužívat stejná čísla na šifrování
- z dvou zpráv zašifrovaných stejným číslem lze lehce získat privátní klíč (whoopsie daisyy)
Kryptografické protokoly
typicky
- výměna nonces
- A generuje master secret
- A posílá m.s. B zašifrované veřejným klíčem B
- A a B podepisují transkript protokolu jejich tajnými klíči
- použijeme KDF pro vytvoření symetrických klíčů z m.s.
- průběh komunikace pomocí symetrické šifry a MAC
- po nějakém čase přegenerováváme symetrické klíče pomocí KDF
2, 3 většinou pomocí DH
Implementační pasti
- fuzzing
- používání C (nebo jiného low-level jazyka)
- šahnu si někam do paměti, kam nemam :(
- nepoužívání C
- jednoduché exploitnout
Side channels
Remote attacker
- timing attack
- např. dotaz na heslo – porovnáváme 2 stringy po znacích
- porovnávání 2 stringů se stejným prefixem bude trvat déle – můžeme měřit
- ambiguous data
- nějaký script se dá schovat např. do komentáře, který se podle různé implementace parserů vykoná nebo ne
- JSON má hned několik standardů ( :sob: )
- XML – má velmi komplexní standard, takže snad žádná implementace parserů není správná
- UTF-8 a Unicode
- format detection
- některý Java bytecode je validní jpeg (pardon??)
- nějaký script se dá schovat např. do komentáře, který se podle různé implementace parserů vykoná nebo ne
- DOS
- zaplavení serveru s nesmyslnými requesty
In the same room
- měření power consumption
- některé instrukce procesoru jsou jinak náročné
- elektromagentický šum
- měření
- sound-based keylogger
- měření teploty/„ošoupanosti” kláves/tlačítek
Physical access
- coldboot attack
- náš běící stroj má nahrané klíče v RAMce… tak ji prostě vytahnem a rychle strčíme k nám
- Trojan horse
- prostě si nahraju na stroj svůj backdoor
Run my code
stačí mít na stránce javascript, hehe
Meltdown
- právě zažívám meltdown a mým procesorem to nebude :sob:
Cache-based AES attack
chosen plaintext
- existuje verze (daleko komplikovanější), která funguje i s known plaintextem
AES má 128b klíč a 10 rund (poslední je :sparkles:speciální:sparkles:)
dřív se na AES používal „výbornej” zrychlovací trýček
stav AES je uložen v tabulce $4 \times 4$

první 3 kroky rundy se dají vyměnit za kombinaci několika lookupů v tabulkách
vezmu 4 bajty $A$, $B$, $C$ a $D$ na hlavní diagonále stavu
konkrétně jsou to lookupy $T_1[A]$, $T_2[B]$, $T_3[C]$ a $T_4[D]$
- $T_i$ jsou nějaké předpočítané 256b tabulky dávající 32b výstup = 4B
- poslední spešl runda používá jen jinej typ tabulek $T_i$
XORtěchto lookupů má 4B, ze kterých postavíme první sloupec výsledku- pro další sloupce jen vezmeme prvky na 1., 2. … vedlejší diagonále (plus cyklicky doplníme)
běžné L1 cache dnešních počítačů mají 64B bloky
- každý blok obsahuje 16 buněk tabulky $T_i$
chosen plaintext: zafixuji $A$, $B$, $C$ a $D$ a zbytek bloku volím naprosto náhodně
- AES je deterministický – zafixované parametry se vždy zacachují na stejné místo
- po několika pokusech je jednodušší měřením rychlosti přístupu zjistit, jak vypadají předpočítané tabulky $T_i$ (teda dozvíme se vždy jen vrchní 4 bity každého bajtu kvůli splitování do nloků cache)
neorzumim tomu, prostě nevim… tak se omlouvám, že je tahle část pěkně trash
ale klidně vám popovídám něco o meltdownu :3
Udržování tajemství
- na disku fakt ne pls
- RAM
- když dojde, začne swapovat věci na disk (hups)
- když crashne, vyhodí core dump
- registry
- mohou skončit v paměti
Hesla
- nejpoužívanější způsob zabezpečení
- většinou ale nejslabší článek celého systému
- lidi jsou trochu dementi
Uchovávání hesel
- hashování hesel
- většinou server-side
Předpočítávání hashů hesel
pokud bychom chtěli crackovat hesla, mohli bychom si předem předpočítat úplně všechny hashe všech možných hesel z univerza a pak jen lookupovat
- to je ale strašně drahý na paměť
chytřejší předpočítávání
- samplovací funkce z hashe vybere náhodné heslo z univerza všech možných hesel
graph LR
password1 -- h --> hash -- sampling function --> password2
- iterováním tohoto procesu stavím řetízky
graph LR
p1 --> p2 --> p3 --> mid:::hidden --> pn
předpočítám si všechny řetízky pokrývající celé univrzum hesel
- pro každý řetízek si pamatuji první a poslední heslo v řetízku
když chceme cracknout heslo, zahashováním se dostaneme na nějakou pozici doprostřed řetízku
doiterujeme se na konec, odtamtud skočíme na začátek a dojdeme zpět k našemu vstupnímu bodu do řetízku
nyní už ale známe předka tohoto bodu, což je hledané heslo
tradeof horšího času za méně paměti
- pokud je délka řetízku $N$, pak máme paměť $\sim \frac {\text{\#hesel}}{N}$ a čas $N$, ne?
- pozor! řetízky se často spojují, ve skutečnosti tak spotřebujeme paměti daleko více
- pokud je délka řetízku $N$, pak máme paměť $\sim \frac {\text{\#hesel}}{N}$ a čas $N$, ne?
Rainbow tables
- pro každou hranu řetízku použijeme jinou samplovací funkci – máme jiné barvy hran
- to komplikuje lookup hesla – když crackujeme, nevíme, kam jsme se zahashovali a tedy jakou samplovací funkci máme použít, abychom pokračovali v našem řetízku
- jednoduše tedy vyzkoušíme všech $N$ možností
- to komplikuje lookup hesla – když crackujeme, nevíme, kam jsme se zahashovali a tedy jakou samplovací funkci máme použít, abychom pokračovali v našem řetízku
- pokud by měly 2 řetízky zkolidovat, pravděpodobně se potkají na hranách jiné bary
- řetízky se nespojí
- nyní máme čas $N^2$ a paměť opravdu cca $\frac {\text{\#hesel}}{N}$

Ochrana proti brute-force útokům
salting
- hashuje se konkatenace hesla a soli – nějaký random string
- obrana proti rainbow-tables
- také není vidět, že 2 uživatelé mají stejné heslo
iterování hashovací funkce
- zpomaluje hashování, čímž ale zpomaluje i brute-force útoky
PBKDF2
password-based key derivation function
odvozená z libovolné pseudonáhodné funkce s klíčem (typicky HMAC)
vstup: salt a délka požadovaného hesla
výstup: $B_1, B_2, \dots , B_n$
konstrukce $B_i$:
- $B_i = U^i_1 \oplus U^i_2 \oplus \dots \oplus U^i_c$
- $U^i_1 = \text{PRF}(\text{passwd}, \text{salt} || i)$
- $U^i_{j+1} = \text{PRF}(\text{passwd}, U^i_j)$
Challenge-response autentikace
sequenceDiagram
participant c as client
participant s as server
c ->> s: login
s ->> c: nonce, salt
c ->> s: HMAC( h( passwd || salt ), nonce )
note right of c: znalost HMAC podpisu nám nepomůže v získávání hashe hesla
note right of c: podpis závisí na nonci, imunní vůči replay útokům
- server si musí pamatovat hash hesla se solí
- pokud ze serveru získáme hash, můžeme předstírat, že jsme klient a provést ten samý protokol
SCRAM
salted challenge-response authentification mechanism
- řešení případu, kdy ukradneme přímo hash hesla ze serveru
setup: vybereme salt a počet iterací
- zahashujeme heslo: $P := \text{PBKDF2}(\text{passwd}, \text{salt}, \text{\#iterací})$
- vyrobíme client key: $K_C := \text{HMAC}(P, \text{nějaký string})$
- vyrobíme server key $K_S := \text{HMAC}(P, \text{ten samý string})$
- server si pamatuje salt, klíč serveru a hash klíče klienta
- klient si nepotřebuje pamatovat nic krom svého klíče
průběh:
sequenceDiagram
participant c as client
participant s as server
c ->> s: login a client-nonce
s ->> c: salt, server-nonce, #iterací
c ->> s: client-proof
note right of c: client-proof = Kc XOR HMAC( h(Kc), transkript )
s ->> c : server-proof
note left of s: server-proof = HMAC( Ks, transkript )
note left of s: nepovinné (myslim)
klient umí jednoduše verifikovat server proof
server si na moment zjistí klientův klíč a pak ho zahodí
- server má $K_c \oplus \text{HMAC}(h(K_c), \text{transkript})$ a pak samotný hash klíče a samotný transkript
- $\oplus$ je inverzní sám k sobě, takže $K_c$ lze zjistit jednoduše
poměrně těžké zamezit timing side-channel attacks
DNSSEC
- secure domain naming system
- DNS – strom doménových jmen
Záznamy
- ve vrcholech doménového stromu
- A, AAAA, MX, …
- delegace subdomén – NS záznamy
- na zónách, nikoliv doménách (trochu rozdíl?)
Ta jakože security část
veřejný klíč domény – uchováván v DNSKEY záznamu
tajným klíčem podepisujeme záznamy – RRSIG záznamy
- podpis je generován pro dvojici jméno + záznam
DS záznamy v „otcovských” doménách
- hash veřejného klíče domény
- jako každý záznam je podepsán otcovskou doménou
změna klíčů
- při změně klíčů máme u domény 2 klíče najednou
- update klíče by znamenalo updatovat celou větev (au)
- řešení: 2 klíče – key signing key a zone signing key
TODO: tady chybí docela velká část o PKI a chain-KDF (a už se mi nechce ji dopisovat, sry)
TLS
transport layer security
- nástupce SSL – secure sockets layer
- SSL 1 → SSL 2 → SSL 3 → TLS 1.0 → TLS 1.1 → TLS 1.2 → TLS 1.3
stream protokol
autentikace, zabezpečení, integrita
používán jako mezivrstva většiny internetových protokolů
HTTPS = HTTP přes TLS
DTLS – datagram TLS (varianta vhodná např. pro použití s UDP)
TLS 1.3
- výměnna klíčů
- typicky Diffie-Hellman na eliptických křivkách
- autentikace
- RSA podpis + certifikát
- šifrování
- předchozí verze šly často rozbít padding orákulem
- AEAD – Authenticated Encryption with Additional Data
- buďto AES v Galois/Counter módu, nebo třeba ChaCha20 + Poly1305
- dohoda na parametrech
- ve verzi 1.3 poměrně omezená – nechceme volit slabé parametry
- můžeme zvolit verzi TLS, grupu pro DH ze seznamu, autentikační mechanismus, šifru ze seznamu
Record protokol
stará se o šifrování a MAC
přidává padding
- takto můžeme přidat více paddingu, než je potřeba, abychom zamezili leakování informací v naší používané šifře
podprotokoly
- handshake
- posílání aplikačních dat
- alert
- posílá se, když se něco pokazí
- také se pošle speciální alert, když chceme ukončit komunikaci
Key schedule
- TLS má několik podčástí, které všechny potřebují nějaké klíče
- založeno na HKDF
- extrakce a expanze – podobné houbovité konstrukci
- nejdříve extrahujeme nějakou kratší sekvenci, kterou následně expandujeme na tak dlouhou, jak potřebujeme
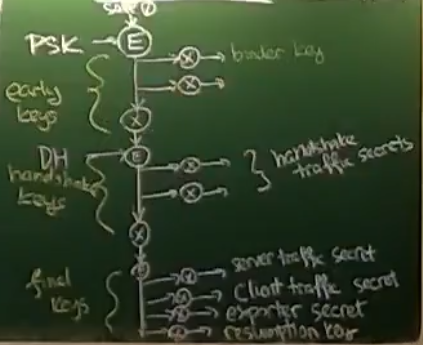
- TLS je nejčastěji používáno pro navázání spojení a vygenerování šifrovacího klíče pro toto spojení
- na to je ten předposlední klíč – exporter secret
Handshake
- před zvolením klíčů nepoužíváme žádné šifrování
sequenceDiagram
participant c as client
participant s as server
c ->> s: Client Hello
Note right of c: key share, nabízené parametry, nabídka PSK
s ->> c: Server Hello
Note left of s: key share, vybrané parametry, vybrané PSK
alt šifrovaná část
s ->> c: Certificate
s ->> c: (Cert Request)
Note left of s: někdy chceme i autentikaci klienta
s ->> c: Cert Verify
Note left of s: podpis dosavadních zpráv certifikovaným klíčem
s ->> c: Finished
s ->> c: Začíná posílat aplikační data
Note left of s: pokud nepotřebujeme autentikaci klienta
c ->> s: <br/><br/><br/> Certificate
c ->> s: Cert Verify
c ->> s: Finished
c ->> s: Začíná posílat aplikační data
end
- další možné zprávy
- ← New session key
- nonce a stav
- klient vyrobí z nonce a resumption key nový PSK (Pre-Security key)
- díky tomuto může server poslat několik noncí a klient může otevřít několik paralelních spojení najednou
- ←→ Key update
- můžeme změnit klíč, nebo požádat druhou stranu, aby změnila klíč
- ← Hello retry
- pokud klient pošle data, která se serveru nelíbí, může jej požádat o nový Client Hello
- ← New session key
Rozšíření
zero-latency handshake
- klient může poslat nějaké další early data
- následně může začít posílat svá data bez čekání na server
- jak ale tato data zabezpečit?
- typicky když obnovujeme ztracené spojení se serverem
- problém: útočník může zachytit client hello včetně early data a znovu jej poslat serveru, který si neukládá historii
- chceme používat jen s idempotentními akcemi (třeba get request), jinak nebezpečné
SNI – Server Name Indication
- jeden server může obsluhovat více domén
- v HTTP můžeme do hlavičky přidat jméno domény, na kterou se ptáme
- přes TLS složité – před výměnou dat musíme ověřit certifikát vázaný na doménové jméno a server zatím neví, na kterou doménu se dotazujeme
- do Client Hello přímo přidáme doménové jméno
- jeden server může obsluhovat více domén
ALPN – Application-Level Protocol Name
- pokud na stejném TCP portu běží více protokolů
- např. chceme na TCP běžet HTTP1 a HTTP2
- klient nabídne protokoly, server jeden vybere
- pokud na stejném TCP portu běží více protokolů
Encrypted Client Hello
- magie
Internet PKI
public key infrastructure
založeno na standardu ITU X.509
- přespříliš komplexní standard
- původně designováno OSI model
Motivace
máme hrozně moc CA
- donedavna pouze komerční, nově i non-profit (např. Let’s Encrypt)
intermediate certificates
- certifikáty pro ověřování certifikátů
- každý je používá jinak
- CA si každý rok vyrobí sama pro sebe nový interm. c. a podepisuje se jím
- delegování ověřování na jinou organizaci
- nemůžeme pak kontrolovat, kolika organizacím takto věříme
- generally to neni dobrej nápad
kdo je přesně svázán s certifikátem?
- podobná jména fake firem
- mnoho i legit firem má ofiko sídlo v daňových rájích a je těžké rozpoznat real firmu od sus firmy
Obsah certifikátu
- jméno držitele
- alternativní jména držitele
- hash veřejného klíče
- kdo certifikát podepsal + podpis
- použití
- platnost od do
- různá rozšíření
Zneplatňování certifikátů
CRL
- Certification Revocation List
- vydává CA
- po chvíli může být fakt velký
- také docela pomalé
Custom revocation list
- seznam velmi důležitých certifikátů udržovaný v prohlížeči
- např certifikáty jednotlivých CA
OCSP
- Onlice Certificate Status Protocol
- protokol, skrz který můžeme kontaktovat CA, jestli je certifikát platný
- problém: pokud útočník odchytí komunikaci, může request zahodit a nedozvíme se nic
- problém2: CA může tímto způsobem hezky monitorovat, které stránky navštěvujeme
OCSP Stapling
- na certifikáty se neptáme my, ale servery
- servery mohou odpovědi cachovat po nějakou krátkou dobu
- můžeme k certifikátu přidat požadavek, že chceme vždy OCSP staple
- moc se ale nepoužívá
Limited lifetime
- nastavíme lifetime dost krátký na to, aby to nevadilo
- např. měsíc
Certificate Transparency project
- mnoho logů
- každý log má seznam všech vydaných certifikátů
- Merkelův strom – těžké měnit historii, lehké přidat data na konec seznamu
- každá CA by měla poslat seznamy svých vydaných certifikátů několika CT logům
- pokud vlastníme doménu, můžeme monitorovat tyto logy
- pokud vidíme log pro naši doménu, který jsme si nevyžádali, vyhlásíme poplach
- historicky některé CA dělaly shady věci a byly tímto způsobem odhaleny
- je to sice jen taková záplata na tenhle zbastlenej certifikační systém, ale je to to nejlepší co máme